Hello,
I am implementing a Nonlinear Model Predictive Controller (NMPC) to control the depth of an underwater vehicle using Acados. However, I am encountering a significant issue where the controller does not accurately track the reference trajectory. Despite setting up the dynamics, cost function, and constraints correctly, the actual trajectory deviates considerably from the reference, and the control inputs do not appear to correct this deviation adequately.
I am using the Python interface of Acados to implement an NMPC controller for controlling the depth of an underwater vehicle.
I aim to:
- Implement an NMPC that tracks a reference depth trajectory accurately.
- Ensure that the controller computes optimal control inputs to minimize tracking errors.
Observed Behavior:
-
The actual trajectory overshoots the reference trajectory and appears to stabilize far from the desired value. However, this stabilization is not intentional. The vehicle reaches the **bottom of the pool, preventing it from diving further.
-
The cost function decreases over time, but the tracking error remains large, indicating that the error term may not be properly minimized in the objective function.
-
Software: Acados with HPIPM as the QP solver.
-
System Dynamics:
- States: z (depth), \dot{z} (velocity).
- Control input: \tau_z (thrust force in the z-direction).
- Nonlinear drag forces are included in the dynamics.
-
Cost Function:
- Weighted least squares (LINEAR_LS) for states and control inputs.
- Reference trajectory is defined for both z and \dot{z}.
-
Constraints:
- Bounds on \tau_z (control input).
-
Prediction Horizon: N=10N , with a sampling time of dt=0.05 seconds.
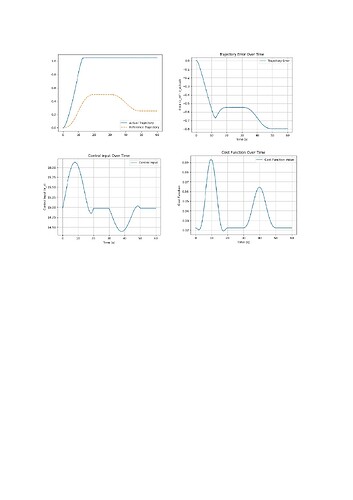
Attached Figures:
- **Actual vs. Reference Trajectory
- Trajectory error
- **Control Inputs
- **Cost Function Evolution
Code Snippet
####Implementation nmpc sur la profondeur pour voir sil ya retard de reception de mesures reelles 10/12/2024
-- coding: utf-8 --
“”"
Created on Tue Dec 10 09:36:12 2024
@author: rbenazouz
“”"
import sys
sys.path.insert(0, ‘/mnt/c/Users/rbenazouz/acados/interfaces/acados_template’)
import time
import socket
import casadi as ca
import numpy as np
import matplotlib.pyplot as plt
from acados_template import AcadosOcp
from acados_template import AcadosOcpSolver
Dynamics
Define the number of states and controls
n_states = 2 # [z, w]
n_controls = 1 # [tau_z]
State and control variables
state = ca.MX.sym(‘state’, n_states)
control = ca.MX.sym(‘control’, n_controls)
Dynamics parameters
z, w = state[0], state[1]
tau_z = control[0]
m = 46.0 # Vehicle mass
g = 9.81 # Gravity
F = 15 # Buoyancy force
B = m * g + F # Total buoyancy force
d_z1 = 22 # Coefficient linéaire de traînée (kg/s)
d_z2 = 800 # Coefficient quadratique de traînée (kg/m)
Simplified dynamics
z_dot = w
drag = d_z1 * z_dot + d_z2 * z_dot**2 # Traînée totale
w_dot = (tau_z - drag * w - F) / m
state_dot = ca.vertcat(z_dot, w_dot)
CasADi dynamics function
f_dynamics = ca.Function(‘f_dynamics’, [state, control], [state_dot])
Discretization of dynamics
dt = 0.05 ## a corrige
NMPC Configuration
ocp = AcadosOcp()
ocp.model.name = ‘depth_control’
ocp.model.x = state
ocp.model.u = control
ocp.model.f_expl_expr = state_dot
ocp.dims.N = 10 # Prediction horizon
ocp.solver_options.tf = ocp.dims.N * dt
Matrices de coût
Q = np.diag([1000000,1000 ]) # Poids pour [z, w] _
R = np.array([[0.001]]) # Poids pour tau_z np.array([[0.001]])
W = np.block([[Q, np.zeros((n_states, n_controls))],
[np.zeros((n_controls, n_states)), R]])
Terminal weight matrix
W_e = Q # Terminal weight matrix
Set cost weights in Acados OCP
ocp.cost.W = W
ocp.cost.W_e = W_e
ocp.cost.W_0 = W
Define selection matrices for cost function
Vx = np.eye(n_states) # Select all states
Vu = np.eye(n_controls) # Select all controls
Vx_e = np.eye(n_states) # Terminal state cost selection
Configurer les références
ocp.cost.cost_type = ‘LINEAR_LS’ # Type de coût (Least Squares)
ocp.cost.cost_type_e = ‘LINEAR_LS’ # Coût terminal
Update cost selection matrices
ocp.cost.Vx = np.vstack([Vx, np.zeros((n_controls, n_states))])
ocp.cost.Vu = np.vstack([np.zeros((n_states, n_controls)), Vu])
ocp.cost.Vx_e = Vx_e
ocp.cost.yref = np.zeros((n_states + n_controls,))
ocp.cost.yref_e = np.zeros((n_states,))
Constraints
ocp.constraints.lbu = np.array([-50.0]) # Lower bound for tau_z
ocp.constraints.ubu = np.array([50.0]) # Upper bound for tau_z
ocp.constraints.idxbu = np.arange(n_controls)
Solver options
ocp.solver_options.qp_solver_tol_stat = 1e-6 # QP solver tolerance for stationarity
ocp.solver_options.qp_solver_tol_eq = 1e-6 # QP solver tolerance for equality constraints
ocp.solver_options.qp_solver_tol_ineq = 1e-6 # QP solver tolerance for inequality constraints
ocp.solver_options.qp_solver_tol_comp = 1e-6 # QP solver tolerance for complementarity
ocp.solver_options.nlp_solver_tol_stat = 1e-6 # NLP tolerance for stationarity
ocp.solver_options.nlp_solver_tol_eq = 1e-6 # NLP tolerance for equality constraints
ocp.solver_options.nlp_solver_tol_ineq = 1e-6 # NLP tolerance for inequality constraints
ocp.solver_options.nlp_solver_tol_comp = 1e-6 # NLP tolerance for complementarity
ocp.solver_options.nlp_solver_max_iter = 1000 # Maximum iterations
Initialize solver
ocp_solver = AcadosOcpSolver(ocp, json_file=‘acados_ocp.json’)
Warm up the NMPC solver
initial_state = np.zeros((n_states,)) # Initial state [z=0, w=0]
ocp_solver.set(0, ‘x’, initial_state) # Set the initial state in the solver
for k in range(ocp.dims.N): # For each prediction horizon step
ocp_solver.set(k, ‘yref’, np.zeros((n_states + n_controls,))) # Set dummy reference
ocp_solver.solve() # Run a warm-up solve to initialize solver’s internal states
t_end = 60
time_array = np.arange(0, t_end, dt)
ZINI, ZINTER, ZF, TF, T_STABLE = 0, 0.5, 0.25, 20.0, 10.0
def poly5_trajectory(t, t_start, t_end, z_start, z_end):
“”"
Generates a 5th-order polynomial trajectory.
:param t: Current time.
:param t_start: Start time.
:param t_end: End time.
:param z_start: Start position.
:param z_end: End position.
:return: Position z(t).
“”"
T = t_end - t_start
if t < t_start:
return z_start, 0.0 # z and its derivative w
elif t > t_end:
return z_end, 0.0 # z and its derivative w
else:
a0 = z_start
a1 = 0
a2 = 0
a3 = 10 * (z_end - z_start) / T3
a4 = -15 * (z_end - z_start) / T4
a5 = 6 * (z_end - z_start) / T5
tau = t - t_start
z_t = a0 + a1 * tau + a2 * tau2 + a3 * tau3 + a4 * tau4 + a5 * tau5
w_t = a1 + 2a2 * tau + 3a3 * tau2 + 4 * a4 * tau3 + 5 * a5 * tau4
return z_t, w_t
Generate reference trajectories
z_trajectory =
w_trajectory =
for t in time_array:
if t < TF:
# Transition from ZINI to ZINTER
z_t, w_t = poly5_trajectory(t, 0, TF, ZINI, ZINTER)
elif t < TF + T_STABLE:
# Steady state at ZINTER
z_t, w_t = ZINTER, 0.01 # Add a small non-zero zdot (w_t)
elif t < 2 * TF + T_STABLE:
# Transition from ZINTER to ZF
z_t, w_t = poly5_trajectory(t, TF + T_STABLE, 2 * TF + T_STABLE, ZINTER, ZF)
else:
# Steady state at ZF
z_t, w_t = ZF, 0.01 # Add a small non-zero zdot (w_t)
z_trajectory.append(z_t)
w_trajectory.append(w_t)
Generate reference trajectories
z_trajectory =
w_trajectory =
for t in time_array:
if t < TF:
z_t, w_t = poly5_trajectory(t, 0, TF, ZINI, ZINTER)
elif t < TF + T_STABLE:
z_t, w_t = ZINTER, 0.0
elif t < 2 * TF + T_STABLE:
z_t, w_t = poly5_trajectory(t, TF + T_STABLE, 2 * TF + T_STABLE, ZINTER, ZF)
else:
z_t, w_t = ZF, 0.0
z_trajectory.append(z_t)
w_trajectory.append(w_t)
The resulting z_trajectory contains the depth reference, and w_trajectory contains the rate of change (velocity) reference.
Start the control loop
start_time = time.time()
Control Loop
Update global index based on elapsed time
Calculate current_time and global_idx
current_time = time.time() - start_time # Elapsed time since the script started
global_idx = int(current_time / dt) # Update global index based on elapsed time
actual_trajectory =
actual_w_trajectory =
control_inputs =
errors =
Initialize storage for plots
control_inputs = # To store control input values
trajectory_errors = # To store trajectory errors
cost_function_values = # To store the cost function values
yref_segments_over_time = # Initialize a list to store yref_segment values
predicted_trajectories =
Initialization Phase
print(“Starting initialization phase…”)
Warm up the NMPC solver
initial_state = np.array([z_trajectory[0], 0.0]) # Match initial depth
Debug: Check the initial state
print(f"Expected initial state: [z = {z_trajectory[0]}, w = 0.0]“)
print(f"Setting initial state in solver: {initial_state}”)
Set the initial state in the solver
ocp_solver.set(0, ‘x’, initial_state)
Debug: Log warm-up references for all prediction horizon steps
for k in range(ocp.dims.N):
yref_debug = np.zeros((n_states + n_controls,))
print(f"Warm-up reference yref at k={k}: {yref_debug}")
ocp_solver.set(k, ‘yref’, yref_debug) # Set dummy reference
Run solver warm-up
print(“Running solver warm-up…”)
status = ocp_solver.solve() # Run a warm-up solve to initialize solver’s internal states
Debug: Check solver status
if status != 0:
print(f"Solver warm-up failed with status {status}. Exiting…")
sys.exit(1)
else:
print(“Solver warm-up completed successfully.”)
print(“Initialization phase complete.”)
Start the control loop
Address and ports for communication
DEST_IP = “192.168.0.17”
DEST_PORT = 5816
Create a UDP socket for receiving robot states
recv_socket = socket.socket(socket.AF_INET, socket.SOCK_DGRAM)
recv_socket.bind((“”, 5825))
print(“Waiting for UDP frames on port 5825…”)
Create a socket for sending control commands
send_socket = socket.socket(socket.AF_INET, socket.SOCK_DGRAM)
recv_socket.settimeout(0.1) # Avoid hanging
Begin Control Loop
Begin Control Loop
while True:
try:
current_time = time.time() - start_time # Elapsed time since control loop started
# Receive current state
try:
recv_time = time.time() # Moment où l'état est reçu
data, address = recv_socket.recvfrom(1024)
#print(f"[{recv_time:.3f}s] Received state: {data.decode('utf-8')}")
except socket.timeout:
print(f"[{time.time():.3f}s] No state received (timeout). Skipping...")
continue # Skip iteration if no data received
fields = data.decode('utf-8').strip().split(',')
if len(fields) < 22 or fields[0] != 'I' or fields[13].strip() != 'J':
print(f"[{current_time:.2f}s] Malformed frame skipped.")
continue
# Extract values
ROV_z = float(fields[3])
ROV_w = float(fields[9]) / 100
#print(f"[{ROV_w:.2f}s] ")
# Set initial state for solver
initial_state = np.array([ROV_z, ROV_w])
ocp_solver.set(0, 'x', initial_state)
print(f"Actual state: {initial_state}")
yref_segment_list = [] # Temporary list to store segments for current time step
# Update reference trajectory
for k in range(ocp.dims.N):
ref_idx = min(global_idx + k, len(z_trajectory) - 1)
yref_segment = np.array([z_trajectory[ref_idx],w_trajectory[ref_idx], 50])
#yref_segment = np.array([z_trajectory[ref_idx],w_trajectory[ref_idx], 0.0])
ocp_solver.set(k, 'yref', yref_segment)
yref_segment_list.append(yref_segment[0]) # Save the depth reference
# Debugging: Print global_idx, ref_idx, and the corresponding value in z_trajectory
#print(f"global_idx: {global_idx}, ref_idx at k={k}: {ref_idx}, z_trajectory[ref_idx]: {z_trajectory[ref_idx]}")
#print(f"At global_idx={global_idx}, ref_idx={ref_idx}, yref_segment={yref_segment}")
print(f"t={current_time:.2f}, z_ref={z_trajectory[global_idx]:.2f}, zdot_ref={w_trajectory[global_idx]:.2f}")
yref_segments_over_time.append(yref_segment_list) # Store all segments for the time step
# Terminal reference
terminal_idx = min(global_idx + ocp.dims.N, len(z_trajectory) - 1)
yref_terminal = np.array([z_trajectory[terminal_idx], 0.0])
ocp_solver.set(ocp.dims.N, 'yref', yref_terminal)
# Solve OCP
status = ocp_solver.solve()
print(f"Solver status at t={current_time:.2f}: {status}")
if status != 0:
print(f"Solver failed with status {status}")
tau_z_optimal = 0.0 # Default to a safe value if solver fails
else:
# Extract optimal control input
tau_z_optimal = ocp_solver.get(0, 'u')[0]
# **Extract Predicted States**:
predicted_states = []
for k in range(ocp.dims.N):
try:
state_k = ocp_solver.get(k, 'x') # Get predicted state at step k
predicted_states.append(state_k)
except Exception as e:
print(f"Error retrieving predicted state at step {k}: {e}")
predicted_states.append(np.nan)
# Convert to numpy array for easier handling
predicted_states = np.array(predicted_states)
# **Debugging**: Print or store predicted states
print(f"Predicted states at t={current_time:.2f}: {predicted_states}")
# **Add Data Collection Here**
# Store control input
control_inputs.append(tau_z_optimal)
# Compute and store trajectory error
error = z_trajectory[global_idx] - ROV_z
trajectory_errors.append(error)
# Retrieve and store cost function value
cost_value = ocp_solver.get_cost()
cost_function_values.append(cost_value)
# Store actual trajectory for analysis
actual_trajectory.append(ROV_z)
# Store actual zdot (w)
actual_w_trajectory.append(ROV_w)
# Send control command
send_time = time.time() # Moment où la commande est envoyée
response_message = f"S,0.00,0.00,{tau_z_optimal:.2f},0.000,0.000,0.000$\n"
send_socket.sendto(response_message.encode('utf-8'), (DEST_IP, DEST_PORT))
#print(f"[{send_time:.3f}s] Sent control command: {response_message.strip()}")
# Update global index
global_idx += 1
if global_idx >= len(z_trajectory):
print("Trajectory complete. Stopping control loop.")
break
except Exception as e:
print(f"Error: {e}")
break