Hi :
I’m building an MPC controller for a simple Ackermann-steering vehicle model to perform point stabilization control,but obtained extremely bizarre output results.The controller is not outputting correct values to guide the car toward the target point; instead, it’s wandering aimlessly.
My model:
Code
x = ca.SX.sym('x')
y = ca.SX.sym('y')
theta = ca.SX.sym('theta')
states = ca.vertcat(x, y, theta)
if self.enable_first_order:
v = ca.SX.sym('v')
w = ca.SX.sym('w')
states = ca.vertcat(states, v, w)
self.nstates = states.size1()
v_cmd = ca.SX.sym('v_cmd')
w_cmd = ca.SX.sym('w_cmd')
controls = ca.vertcat(v_cmd, w_cmd)
self.ncontrols = controls.size1()
if not self.enable_first_order:
rhs = ca.vertcat(
v_cmd * ca.cos(theta),
v_cmd * ca.sin(theta),
w_cmd
)
else:
rhs = ca.vertcat(
v * ca.cos(theta),
v * ca.sin(theta),
w,
(v_cmd - v) / self.tau_v,
(w_cmd - w) / self.tau_w,
)
xdot = ca.SX.sym('xdot', rhs.size1())
# Target point parameters
x_target = ca.SX.sym('x_target')
y_target = ca.SX.sym('y_target')
theta_target = ca.SX.sym('theta_target')
# Obstacle parameters (assume up to 3 obstacles)
x_obs1, y_obs1, r_obs1 = ca.SX.sym('x_obs1'), ca.SX.sym('y_obs1'), ca.SX.sym('r_obs1')
x_obs2, y_obs2, r_obs2 = ca.SX.sym('x_obs2'), ca.SX.sym('y_obs2'), ca.SX.sym('r_obs2')
x_obs3, y_obs3, r_obs3 = ca.SX.sym('x_obs3'), ca.SX.sym('y_obs3'), ca.SX.sym('r_obs3')
obs_num = ca.SX.sym('obs_num') # Actual number of obstacles
# Combine all parameters into a single vector
parameters = ca.vertcat(
x_target, y_target, theta_target,
x_obs1, y_obs1, r_obs1,
x_obs2, y_obs2, r_obs2,
x_obs3, y_obs3, r_obs3,
obs_num
)
self.nparams = parameters.size1()
# Hard constraints
h = [
(x - x_obs1)**2 + (y - y_obs1)**2 - (r_obs1 + self.safe_distance)**2,
(x - x_obs2)**2 + (y - y_obs2)**2 - (r_obs2 + self.safe_distance)**2,
(x - x_obs3)**2 + (y - y_obs3)**2 - (r_obs3 + self.safe_distance)**2,
w_cmd**2 - self.w_gain**2 * v_cmd**2
]
# Obstacle cost
obs_cost = 0
if self.enable_obs:
for i in range(3):
dist_sqr = (states[:2] - parameters[3+3*i:5+3*i]).T @ (states[:2] - parameters[3+3*i:5+3*i])
sigmoid_factor = 1 / (1 + ca.exp((dist_sqr - (self.safe_distance - parameters[5+3*i])**2) * 0.5))
obs_cost += ca.if_else(i < obs_num, self.obs_weight * sigmoid_factor, 0)
model = AcadosModel()
model.name = 'origin_car_model'
model.p = parameters
model.x = states
model.u = controls
model.f_expl_expr = rhs
model.f_impl_expr = xdot - rhs
model.cost_expr_ext_cost = self.Q_x * (x - x_target)**2 + self.Q_y * (y - y_target)**2 \
+ self.Q_theta * (ca.arctan2(ca.sin(theta - theta_target), ca.cos(theta - theta_target)))**2 \
+ self.R_v * v_cmd**2 + self.R_w * w_cmd**2 + obs_cost
model.cost_expr_ext_cost_e = 10 * (self.Q_x * (x - x_target)**2 + self.Q_y * (y - y_target)**2 \
+ self.Q_theta * (ca.arctan2(ca.sin(theta - theta_target), ca.cos(theta - theta_target)))**2)
model.con_h_expr = ca.vertcat(*h)
My OCP configuration code is as follows:
Code
os.chdir(os.path.dirname(os.path.realpath(__file__)))
acados_source_path = os.environ['ACADOS_SOURCE_DIR']
sys.path.insert(0, acados_source_path)
ocp = AcadosOcp()
ocp.model = model
ocp.acados_include_path = acados_source_path + '/include'
ocp.acados_lib_path = acados_source_path + '/lib'
ocp.dims.N = self.N
ocp.dims.np = self.nparams
ocp.dims.nx = self.nstates
ocp.dims.nu = self.ncontrols
ocp.dims.nh = 4
# Initial parameter values
ocp.parameter_values = np.array([
0.0, 0.0, 0.0,
1e10, 1e10, 0,
1e10, 1e10, 0,
1e10, 1e10, 0,
0
])
# Set constraints
ocp.constraints.lh = np.array([0.0] * 3 + [-1e10])
ocp.constraints.uh = np.array([1e10] * 3 + [0])
ocp.constraints.x0 = np.zeros(self.nstates)
ocp.constraints.lbx = np.array([0, 0, -np.pi])
ocp.constraints.ubx = np.array([5, 5, np.pi])
ocp.constraints.idxbx = np.array([0, 1, 2])
if self.enable_first_order:
ocp.constraints.lbx = np.append(ocp.constraints.lbx, [self.v_min, -self.v_max * self.w_gain])
ocp.constraints.ubx = np.append(ocp.constraints.ubx, [self.v_max, self.v_max * self.w_gain])
ocp.constraints.idxbx = np.array([0, 1, 2, 3, 4])
ocp.constraints.lbu = np.array([self.v_min, -self.v_max * self.w_gain])
ocp.constraints.ubu = np.array([self.v_max, self.v_max * self.w_gain])
ocp.constraints.idxbu = np.array([0, 1])
ocp.cost.cost_type = 'EXTERNAL'
ocp.cost.cost_type_e = 'EXTERNAL'
ocp.solver_options.tf = self.N * self.dt
ocp.solver_options.N_horizon = self.N
ocp.solver_options.qp_solver = 'PARTIAL_CONDENSING_HPIPM'
ocp.solver_options.nlp_solver_type = 'SQP_RTI'
ocp.solver_options.nlp_solver_max_iter = self.max_iter
ocp.solver_options.tol = self.solver_tol
ocp.solver_options.hessian_approx = 'GAUSS_NEWTON'
ocp.solver_options.ext_cost_num_hess = True
ocp.solver_options.integrator_type = 'ERK'
ocp.solver_options.print_level = 0
os.makedirs("./Origin_car_model_cfg", exist_ok=True)
try:
solver = AcadosOcpSolver(ocp, json_file="./car_model_cfg/_acados_ocp.json", generate=True, build=True)
except Exception as e:
print(f"Failed to create solver: {e}")
return
for i in range(ocp.dims.N + 1):
solver.set(i, 'x', np.zeros(self.nstates))
for i in range(ocp.dims.N):
solver.set(i, 'u', np.zeros(self.ncontrols))
return solver
My control function:
start_time = time.time()
# Set initial state constraints
self.solver.set(0, 'lbx', current_states)
self.solver.set(0, 'ubx', current_states)
self.solver.set(0, 'x', current_states)
# Fill in obstacle parameters
obs_params = np.array([
1e10, 1e10, 0,
1e10, 1e10, 0,
1e10, 1e10, 0,
0
])
if self.enable_obs:
for i in range(len(obs)):
obs_params[0+i*3] = obs[i][0]
obs_params[1+i*3] = obs[i][1]
obs_params[2+i*3] = obs[i][2]
obs_params[-1] = len(obs)
params = np.append(target_point, obs_params)
for i in range(self.N + 1):
self.solver.set(i, 'p', params)
self.solver.solve()
v_cmd = self.solver.get(0, 'u')[0]
w_cmd = self.solver.get(0, 'u')[1]
print(f"Solver time: {time.time() - start_time}s")
return v_cmd, w_cmd
Complete code:
class MPCController:
"""
Ackermann steering vehicle controller based on nonlinear Model Predictive Control (MPC)
"""
def __init__(self, config: Dict[str, Any]):
"""
Initialize the MPC controller
Args:
config: Configuration dictionary containing MPC parameters
"""
# System model settings
self.enable_first_order = config.get('enable_first_order', False)
# Control parameters
self.dt = config.get('dt', 0.1) # Control period (s)
self.N = config.get('horizon', 10) # Prediction horizon length
self.Q_x = config.get('Q_x', 10.0) # Weight for x position error
self.Q_y = config.get('Q_y', 10.0) # Weight for y position error
self.Q_theta = config.get('Q_theta', 5.0) # Weight for heading angle error
self.R_v = config.get('R_v', 1.0) # Weight for linear velocity control input
self.R_w = config.get('R_w', 1.0) # Weight for angular velocity control input
self.v_target = config.get('v_target', 1.0) # Target velocity (m/s)
self.Q_v = config.get('Q_v', 2) # Weight for velocity tracking error
# Constraint parameters
self.v_max = config.get('v_max', 0.8) # Maximum linear velocity (m/s)
self.v_min = config.get('v_min', -0.5) # Minimum linear velocity (m/s)
self.w_gain = config.get('w_gain', 3.0) # Proportional gain between angular and linear velocity
# First-order dynamic response parameters
self.tau_v = config.get('tau_v', 0.8) # Time constant for linear velocity response
self.tau_w = config.get('tau_w', 0.8) # Time constant for angular velocity response
# Solver parameters
self.max_iter = config.get('max_iter', 100) # Maximum number of iterations
self.solver_tol = config.get('solver_tol', 1e-8) # Solver tolerance
# Obstacle avoidance parameters
self.enable_obs = config.get('enable_obs', False)
self.max_obs_num = config.get('max_obs_num', 3)
self.obs_weight = config.get('obs_weight', 5)
self.safe_distance = config.get('safe_distance', 0.2)
# Initialize solver
self._setup_solver()
print("Solver initialization complete")
# Previous control inputs for computing control change rate
self.u_prev = np.array([0.0, 0.0] * self.N)
def _setup_solver(self):
model = self.AkmCarModel()
self.solver = self.configure_ocp(model)
def AkmCarModel(self):
x = ca.SX.sym('x')
y = ca.SX.sym('y')
theta = ca.SX.sym('theta')
states = ca.vertcat(x, y, theta)
if self.enable_first_order:
v = ca.SX.sym('v')
w = ca.SX.sym('w')
states = ca.vertcat(states, v, w)
self.nstates = states.size1()
v_cmd = ca.SX.sym('v_cmd')
w_cmd = ca.SX.sym('w_cmd')
controls = ca.vertcat(v_cmd, w_cmd)
self.ncontrols = controls.size1()
if not self.enable_first_order:
rhs = ca.vertcat(
v_cmd * ca.cos(theta),
v_cmd * ca.sin(theta),
w_cmd
)
else:
rhs = ca.vertcat(
v * ca.cos(theta),
v * ca.sin(theta),
w,
(v_cmd - v) / self.tau_v,
(w_cmd - w) / self.tau_w,
)
xdot = ca.SX.sym('xdot', rhs.size1())
# Target point parameters
x_target = ca.SX.sym('x_target')
y_target = ca.SX.sym('y_target')
theta_target = ca.SX.sym('theta_target')
# Obstacle parameters (assume up to 3 obstacles)
x_obs1, y_obs1, r_obs1 = ca.SX.sym('x_obs1'), ca.SX.sym('y_obs1'), ca.SX.sym('r_obs1')
x_obs2, y_obs2, r_obs2 = ca.SX.sym('x_obs2'), ca.SX.sym('y_obs2'), ca.SX.sym('r_obs2')
x_obs3, y_obs3, r_obs3 = ca.SX.sym('x_obs3'), ca.SX.sym('y_obs3'), ca.SX.sym('r_obs3')
obs_num = ca.SX.sym('obs_num') # Actual number of obstacles
# Combine all parameters into a single vector
parameters = ca.vertcat(
x_target, y_target, theta_target,
x_obs1, y_obs1, r_obs1,
x_obs2, y_obs2, r_obs2,
x_obs3, y_obs3, r_obs3,
obs_num
)
self.nparams = parameters.size1()
# Hard constraints
h = [
(x - x_obs1)**2 + (y - y_obs1)**2 - (r_obs1 + self.safe_distance)**2,
(x - x_obs2)**2 + (y - y_obs2)**2 - (r_obs2 + self.safe_distance)**2,
(x - x_obs3)**2 + (y - y_obs3)**2 - (r_obs3 + self.safe_distance)**2,
w_cmd**2 - self.w_gain**2 * v_cmd**2
]
# Obstacle cost
obs_cost = 0
if self.enable_obs:
for i in range(3):
dist_sqr = (states[:2] - parameters[3+3*i:5+3*i]).T @ (states[:2] - parameters[3+3*i:5+3*i])
sigmoid_factor = 1 / (1 + ca.exp((dist_sqr - (self.safe_distance - parameters[5+3*i])**2) * 0.5))
obs_cost += ca.if_else(i < obs_num, self.obs_weight * sigmoid_factor, 0)
model = AcadosModel()
model.name = 'origin_car_model'
model.p = parameters
model.x = states
model.u = controls
model.f_expl_expr = rhs
model.f_impl_expr = xdot - rhs
model.cost_expr_ext_cost = self.Q_x * (x - x_target)**2 + self.Q_y * (y - y_target)**2 \
+ self.Q_theta * (ca.arctan2(ca.sin(theta - theta_target), ca.cos(theta - theta_target)))**2 \
+ self.R_v * v_cmd**2 + self.R_w * w_cmd**2 + obs_cost
model.cost_expr_ext_cost_e = 10 * (self.Q_x * (x - x_target)**2 + self.Q_y * (y - y_target)**2 \
+ self.Q_theta * (ca.arctan2(ca.sin(theta - theta_target), ca.cos(theta - theta_target)))**2)
model.con_h_expr = ca.vertcat(*h)
return model
def configure_ocp(self, model):
os.chdir(os.path.dirname(os.path.realpath(__file__)))
acados_source_path = os.environ['ACADOS_SOURCE_DIR']
sys.path.insert(0, acados_source_path)
ocp = AcadosOcp()
ocp.model = model
ocp.acados_include_path = acados_source_path + '/include'
ocp.acados_lib_path = acados_source_path + '/lib'
ocp.dims.N = self.N
ocp.dims.np = self.nparams
ocp.dims.nx = self.nstates
ocp.dims.nu = self.ncontrols
ocp.dims.nh = 4
# Initial parameter values
ocp.parameter_values = np.array([
0.0, 0.0, 0.0,
1e10, 1e10, 0,
1e10, 1e10, 0,
1e10, 1e10, 0,
0
])
# Set constraints
ocp.constraints.lh = np.array([0.0] * 3 + [-1e10])
ocp.constraints.uh = np.array([1e10] * 3 + [0])
ocp.constraints.x0 = np.zeros(self.nstates)
ocp.constraints.lbx = np.array([0, 0, -np.pi])
ocp.constraints.ubx = np.array([5, 5, np.pi])
ocp.constraints.idxbx = np.array([0, 1, 2])
if self.enable_first_order:
ocp.constraints.lbx = np.append(ocp.constraints.lbx, [self.v_min, -self.v_max * self.w_gain])
ocp.constraints.ubx = np.append(ocp.constraints.ubx, [self.v_max, self.v_max * self.w_gain])
ocp.constraints.idxbx = np.array([0, 1, 2, 3, 4])
ocp.constraints.lbu = np.array([self.v_min, -self.v_max * self.w_gain])
ocp.constraints.ubu = np.array([self.v_max, self.v_max * self.w_gain])
ocp.constraints.idxbu = np.array([0, 1])
ocp.cost.cost_type = 'EXTERNAL'
ocp.cost.cost_type_e = 'EXTERNAL'
ocp.solver_options.tf = self.N * self.dt
ocp.solver_options.N_horizon = self.N
ocp.solver_options.qp_solver = 'PARTIAL_CONDENSING_HPIPM'
ocp.solver_options.nlp_solver_type = 'SQP_RTI'
ocp.solver_options.nlp_solver_max_iter = self.max_iter
ocp.solver_options.tol = self.solver_tol
ocp.solver_options.hessian_approx = 'GAUSS_NEWTON'
ocp.solver_options.ext_cost_num_hess = True
ocp.solver_options.integrator_type = 'ERK'
ocp.solver_options.print_level = 0
os.makedirs("./Origin_car_model_cfg", exist_ok=True)
try:
solver = AcadosOcpSolver(ocp, json_file="./Origin_car_model_cfg/_acados_ocp.json", generate=True, build=True)
except Exception as e:
print(f"Failed to create solver: {e}")
return
for i in range(ocp.dims.N + 1):
solver.set(i, 'x', np.zeros(self.nstates))
for i in range(ocp.dims.N):
solver.set(i, 'u', np.zeros(self.ncontrols))
return solver
def control(self, current_states, target_point: np.ndarray, obs: List):
start_time = time.time()
# Set initial state constraints
self.solver.set(0, 'lbx', current_states)
self.solver.set(0, 'ubx', current_states)
self.solver.set(0, 'x', current_states)
# Fill in obstacle parameters
obs_params = np.array([
1e10, 1e10, 0,
1e10, 1e10, 0,
1e10, 1e10, 0,
0
])
if self.enable_obs:
for i in range(len(obs)):
obs_params[0+i*3] = obs[i][0]
obs_params[1+i*3] = obs[i][1]
obs_params[2+i*3] = obs[i][2]
obs_params[-1] = len(obs)
params = np.append(target_point, obs_params)
for i in range(self.N + 1):
self.solver.set(i, 'p', params)
self.solver.solve()
v_cmd = self.solver.get(0, 'u')[0]
w_cmd = self.solver.get(0, 'u')[1]
print(f"Solver time: {time.time() - start_time}s")
return v_cmd, w_cmd
mpc = MPCController({})
print('v_cmd,w_cmd:',mpc.control(np.array([0.0,0.0,0.0,0.0,0.0]),np.array([0.001,0.001,0]),[])[0:2],)
When I input a target point extremely close to the starting point (e.g., current_states = [0,0,0,0,0] , target point [0.0001, 0.0001] or [0.00001, 0.0001] ), the controller outputs unreasonable values like a linear velocity exceeding 0.6 , causing erratic behavior.
output
Solver time:0.0013821125030517578s
v_cmd,w_cmd: (np.float64(0.6795298852283124), np.float64(0.0))
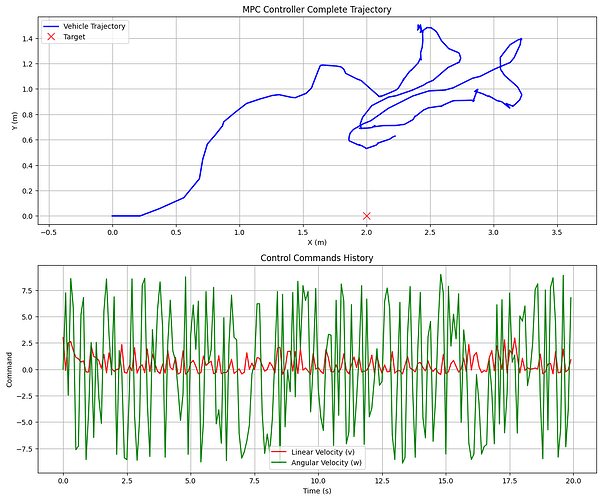
The trajectory in my simulation program is extremely bizarre.
When first order enable:
When first order disable:
The car is spinning in place (instead of converging to the target).
with:
SQP_RTI: QP solver returned error status 3 QP iteration 23.
Is the issue in my model design or solver settings ?
!I successfully implemented control of my model using the LINEARLS cost type, and it works well with both SQP and SQP_RTI solvers. However, the EXTERN cost type still fails. Could this be due to the introduction of non-differentiable functions like arctan2? Additionally, when using the SQP/SQP_RTI solvers, I observed significant output oscillations, and the robot’s trajectory exhibits minor wobbling (especially in point-to-point control over longer distances), unlike the IPOPT solver which moves straight to the target after turning. Would specifying a reference path resolve this issue?