Hi I am very new to the field of optimization and l am learning to formulate problems in acados and Casadi.
I have a quad rotor model simulation, where I already have it moving from a starting position to a final position.
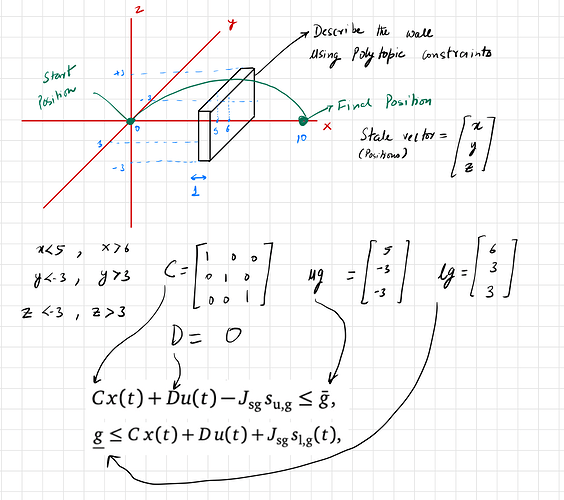
Now I want to add a wall in the 3D space so that the quad rotor has to maneuverer around it. I was trying to do that by using the polytopic path constraint in the formulation as follows. I have defined matrix C, D and constant vectors ‘lg’ and ‘ug’ as follows.
Can someone comment on this approach? Is this even the right way to approach this? or is there any other more efficient way to do this?
Thanks
Gurpreet
Hi Gurpreet,
Personally I do not think this is the right way to approach. You should notice that staying within a polytope can be formulated as linear constraints:
A_1 x + b_1 \leq 0 \quad \textrm{and} \quad A_2 x + b_2 \leq 0 \quad ... \quad \textrm{and} \quad A_m x + b_m \leq 0
which can certainty be written in the form of Cx + Du \leq g and gives you a convex set.
However, if you want to stay out of this polytope, the constraints should be formulated as the following:
A_1 x + b_1 >0 \quad \textrm{or} \quad A_2 x + b_2 > 0 \quad ... \quad \textrm{or} \quad A_m x + b_m >0
It’s important to notice here we have OR rather than AND, which reflects the non-convex and combinatorial nature of such constraints.
I’m not an expert in this, but in my limited knowledge solving such problems in real-time is challenging. In your case if you do not have too much obstacles, maybe you can look into Mixed Integer Programming (MIP). I think acados doesn’t provide direct support to Mixed Integer Programming, but maybe you can still use acados to solve sub-problems after you do branch and bound. Or maybe you should look for other solvers that can handle MIP.