Hi ![]()
I am currently converting my NMPC that was formulated in casadi to acados using the matlab interface, as ACADOS offers code generation and simulink support via the S-Functions. Which is great! So thanks for this great tool!
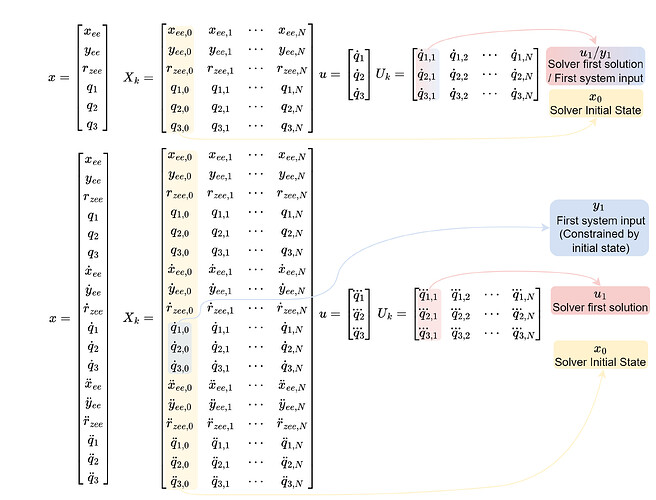
In my casadi implementation my optimization variables where my states and inputs over my prediction horizon N. So for example say my system (in simplified version) is described like this:
Then my optimization variables that I use are like this:
Previously I had access to all these states at the same time while building my solver, however as I understand it, in acados you build your code for each shooting node step of the full prediction horizon in one go (except for the terminal cost and constraints etcetera that you can set).
Most of my code I can reformulate to the acados formulation (which makes the formulation simpler which is nice!). However I am struggling with two particular problems.
Problem 1: Accessing inputs from other shooting steps
In my code I impose constraints on the states, the velocities(the inputs), the acceleration and jerks. Imposing the constraints on my states is and velocities is easy to do in acados. I am however unsure how to do this. For example this code represents how I do it in my casadi implementation.
N = 21;% Number of shooting nodes steps (prediction horizon length)
l_b_acc = -0.5; % lower bound for the acceleration
u_b_acc = 0.5; % upper bound for the acceleration
for k = 1 : N
if k == 1
h(k) = (U(k) - P(nx+1)) /Ts; %Take previous input stored in parameter vector
else
h(k) = (U(k) - U(k-1))/Ts; %Differentiate to approximate acceleration
end
end
% Similar approach for the joint jerks, and then afterwards the bounds are set as constraints.
At least to my understanding this is not possible in acados as you define your problem for one shooting node step, which is then applied over the full horizon.
Is there however a way to communicate in between these steps, for example passing the previous input shooting step input, such that I can constrain my acceleration in similar fashion?
Problem 2: Setting parameter vector for individual shooting step
My cost function does not fit the standard linear or non-linear least squares module form, thus I am using the ext_cost functionality. Part of my full objective cost is however a least squares term for the reference tracking over the horizon. Here I substract my joint velocities from the desired velocities. How can I best pass this vector with desired velocities my y_ref basically to my problem considering my use of the ext_cost.
I have for now implemented it by adding my reference signal to my parameter vector that I pass as an argument for solving. Like this:
yr = p(nx+nu+1+(1-1)*nx_e : nx + nu +1*nx_e); % retrieval of reference velocity from parameter vector
sym_p = [p, yr]; % paste it at back of parameter vector for easy access sym_p(end)
ocp.set('p', sym_p'); % set it for use in solving the ocp.
This functions with correct velocity reference tracking. However this means that my reference now needs to be constant over the full horizon, which is not desirable. In the documentation of the python interface it is mentioned that one can set the parameter vector for a specific shooting node step using this input:
`set` (*stage_: int* , *field_: str* , *value_: numpy.ndarray* )
For the matlab interface this is not documented, but looking at the functions itself it is defined slightly differently:
function set(obj, field, value, varargin)
obj.t_ocp.set(field, value, varargin{:});
end
Therefore I tried this approach where I retrieve the relevant desired velocity for the shooting node from my parameters vector p, and then paste it again at the back (this way in my code I could just set, desired velocity is sym_p(end)) :
for i = 1:N
yr = p(nx+nu+1+(i-1)*nx_e : nx + nu + i*nx_e); % retrieval of reference velocity from parameter vector
sym_p = [p, yr]; % paste it at back of parameter vector for easy access sym_p(end)
ocp.set('p', sym_p', i); % set it for use in solving the ocp for shooting node step i
end
This approach does not work (the reference tracking is not present). What am I doing wrong here? And is there perhaps a better way to approach this?
If anyone knows how to tackle these two problems that would be wonderful! Thanks in advance!
Kind regards,
Tim