Hi ![]()
I am new to ACADOS and MPC in general.
I am trying to implement Acados numerical solver for finding the solution of the MPC problem for trajectory optimization of a Mobile robot
I am using Python interface and I want to implement two different cost functions:
- The cost function of minimizing the error between real and initial trajectory has the following general formula
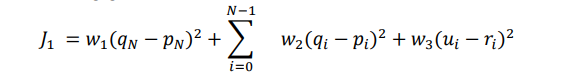
where
- q and u are the output and input vectors of the trajectory of the robot
- p and r are the output and input vector of the trajectory,
- w_1 , w_2 , w_3 are weights.
- Control inputs are r = [a, w]^T=0
- Cost function for avoiding obstacles:

I was told to use NONLINEAR_LS for defining the cost functions. but I am not sure how to combine two different costs.
My code:
Model
def mobile_robot_model():
model_name = 'mobile_robot'
# Define symbolic variables (states)
x = ca.MX.sym('x')
y = ca.MX.sym('y')
v = ca.MX.sym('v')
theta = ca.MX.sym('theta')
# Control
a = ca.MX.sym('a') # acceleration
w = ca.MX.sym('w') # angular velocity
# Define state and control vectors
states = ca.vertcat(x, y, v, theta)
controls = ca.vertcat(a, w)
rhs = [v*ca.cos(theta), v*ca.sin(theta), a, w]
x_dot = ca.MX.sym('x_dot', len(rhs))
# Create a CasADi function for the continuous-time dynamics
continuous_dynamics = ca.Function(
'continuous_dynamics',
[states, controls],
[ca.vcat(rhs)],
["state", "control_input"],
["rhs"]
)
f_impl = x_dot - continuous_dynamics(states, controls)
model = AcadosModel()
model.f_expl_expr = continuous_dynamics(states, controls)
model.f_impl_expr = f_impl
model.x = states
model.xdot = x_dot
model.u = controls
model.p = []
model.name = model_name
return model
Solver:
def create_ocp_solver():
# Create AcadosOcp object
ocp = AcadosOcp()
# Set up the optimization problem
model = mobile_robot_model()
ocp.model = model
# --------------------PARAMETERS--------------
# constants
nx = model.x.size()[0]
nu = model.u.size()[0]
T = 30
N = 100
n_params = len(model.p)
# Setting initial conditions
ocp.dims.N = N
ocp.dims.nx = nx
ocp.dims.nu = nu
ocp.solver_options.tf = T
# initial state
x_ref = np.zeros(nx)
# Set initial condition for the robot
ocp.constraints.x0 = x_ref
# initialize parameters
ocp.dims.np = n_params
ocp.parameter_values = np.zeros(n_params)
# ---------------------CONSTRAINTS------------------
# Define constraints on states and control inputs
ocp.constraints.lbu = np.array([-0.1, -0.3]) # Lower bounds on control inputs
ocp.constraints.ubu = np.array([0.1, 0.3]) # Upper bounds on control inputs
ocp.constraints.lu = np.array([100, 100, 1, 10]) # Upper bounds on states
ocp.constraints.idxbu = np.array([0, 1]) # for indices 0 & 1
# ---------------------COSTS--------------------------
# Define J1 and J2
# Define cost_y_expr, cost_y_expr_e
# Define W and W_e
# Define yref and yref_e
ocp.cost.cost_type = 'NONLINEAR_LS'
ocp.cost.cost_type_e = 'NONLINEAR_LS'
X = ocp.model.x
U = ocp.model.u
# Cost weights
w1 = 1.0 # adjust as needed
w2 = 1.0 # adjust as needed
w3 = 1.0 # adjust as needed
w = 1.0
J2 = obstacle_cost(X, w)
# Parameters:
ocp.model.cost_y_expr = J2
ocp.model.cost_y_expr_e = J2
ocp.cost.W = np.eye(1)
ocp.cost.W_e = np.eye(1)
ocp.cost.yref = np.array([0])
ocp.cost.yref_e = np.array([0])
# ---------------------SOLVER-------------------------
ocp.solver_options.qp_solver = 'PARTIAL_CONDENSING_HPIPM'
ocp.solver_options.hessian_approx = 'GAUSS_NEWTON'
ocp.solver_options.integrator_type = 'ERK'
ocp.solver_options.nlp_solver_type = 'SQP_RTI'
# Set up Acados solver
acados_solver = AcadosOcpSolver(ocp, json_file='acados_ocp.json')
acados_integrator = AcadosSimSolver(ocp, json_file='acados_ocp.json')
return ocp, acados_solver, acados_integrator
I have implemented the cost function for obstacles but not for the trajectory.
Thank you for the help ![]()