Hi ![]()
I imitate minimal_example_ocp to write matlab code to solve my own model.
model code:
function model = hydraulic_sys_no_load_model(varargin)
import casadi.*
%% system dimensions
nx = 6;
nu = 3;
%% system parameters
m = 400;
Bp = 1024361;
F = 65637;
E1 = 1e9;
E2 = 1889610693;
Cv = 0.0018;
Lv = 0.016617;
Vp0 = 0.0263848;
Vc0 = 0.0018;
wv = 87;
ksi = 0.8;
kv = 0.000537;
A = 0.02356;
%% named symbolic variables
xc = SX.sym('xc');
vc = SX.sym('vc');
pp = SX.sym('pp');
pc = SX.sym('pc');
xv = SX.sym('xv');
vv = SX.sym('vv');
w = SX.sym('w');
r = SX.sym('r');
v = SX.sym('v');
%% (unnamed) symbolic variables
x = vertcat(xc, vc, pp, pc, xv, vv);
xdot = SX.sym('xdot', nx, 1);
u = vertcat(w, r, v);
f_expl_expr = vertcat(vc, ...
(A*pc + 10*m - Bp*vc - F)/m, ...
E1*((6.366e-7)*w*r - Cv*Lv*atan(v)*xv*sqrt(pp-pc))/Vp0, ...
E2*(Cv*Lv*atan(v)*xv*sqrt(pp-pc) - A*vc)/(Vc0 + A*xc), ...
vv, ...
-(wv^2)*xv - 2*ksi*wv*vv + kv*(wv^2)*v);
f_impl_expr = f_expl_expr - xdot;
% discrete dynamics
if nargin > 0
delta_t = varargin{1};
disc_dyn_expr = x + delta_t * f_expl_expr; % explicit Euler
else
disc_dyn_expr = [];
end
% populate
model = AcadosModel();
model.x = x;
model.xdot = xdot;
model.u = u;
model.f_expl_expr = f_expl_expr;
model.f_impl_expr = f_impl_expr;
model.disc_dyn_expr = disc_dyn_expr;
model.name = 'hydraulic';
end
ocp solver code:
import casadi.*
% options needed for the Simulink example
if ~exist('simulink_opts','var')
% disp('using acados simulink default options')
% simulink_opts = get_acados_simulink_opts;
disp('using empty simulink_opts to generate solver without simulink block')
simulink_opts = [];
end
check_acados_requirements()
%% solver settings
N = 20; % number of discretization steps
T = 1; % [s] prediction horizon length
x0 = [0; 0; 5345000; 3200000; 0; 0]; % initial state
%% model dynamics
model = hydraulic_sys_no_load_model();
nx = length(model.x); % state size
nu = length(model.u); % input size
%% OCP formulation object
ocp = AcadosOcp();
ocp.model = model;
%% cost in nonlinear least squares form
W_x = diag([1e3, 1e3, 1e-2, 1e-2, 1e-2, 1e-2]);
W_u = diag([1e-2, 1e-2, 1e-2]);
% initial cost term
ny_0 = nu;
ocp.cost.cost_type_0 = 'NONLINEAR_LS';
ocp.cost.W_0 = W_u;
ocp.cost.yref_0 = zeros(ny_0, 1);
ocp.model.cost_y_expr_0 = model.u;
% path cost term
ny = nx + nu;
ocp.cost.cost_type = 'NONLINEAR_LS';
ocp.cost.W = blkdiag(W_x, W_u);
ocp.cost.yref = zeros(ny, 1);
ocp.model.cost_y_expr = vertcat(model.x, model.u);
% terminal cost term
ny_e = nx;
ocp.cost.cost_type_e = 'NONLINEAR_LS';
ocp.model.cost_y_expr_e = model.x;
ocp.cost.yref_e = zeros(ny_e, 1);
ocp.cost.W_e = W_x;
%% define constraints
% only bound on u on initial stage and path
ocp.model.con_h_expr = model.u;
ocp.model.con_h_expr_0 = model.u;
U_max = [157; 10; 10];
U_min = [0; 0; 0];
ocp.constraints.lh = U_min;
ocp.constraints.lh_0 = U_min;
ocp.constraints.uh = U_max;
ocp.constraints.uh_0 = U_max;
ocp.constraints.x0 = x0;
% define solver options
ocp.solver_options.N_horizon = N;
ocp.solver_options.tf = T;
ocp.solver_options.nlp_solver_type = 'SQP';
ocp.solver_options.integrator_type = 'IRK';
ocp.solver_options.qp_solver = 'PARTIAL_CONDENSING_HPIPM';
ocp.solver_options.qp_solver_mu0 = 1e3;
ocp.solver_options.qp_solver_cond_N = 5;
ocp.solver_options.hessian_approx = 'GAUSS_NEWTON';
% ocp.solver_options.ext_fun_compile_flags = '-O2';
ocp.solver_options.globalization = 'MERIT_BACKTRACKING';
% ocp.solver_options.qp_solver_iter_max = 100
ocp.simulink_opts = simulink_opts;
% create solver
ocp_solver = AcadosOcpSolver(ocp);
% solver initial guess
x_traj_init = zeros(nx, N+1);
x_traj_init(1,:) = 0.3;
u_traj_init = zeros(nu, N);
%% call ocp solver
% update initial state
ocp_solver.set('constr_x0', x0);
% set trajectory initialization
ocp_solver.set('init_x', x_traj_init); % states
ocp_solver.set('init_u', u_traj_init); % inputs
ocp_solver.set('init_pi', zeros(nx, N)); % multipliers for dynamics equality constraints
% change values for specific shooting node using:
% ocp_solver.set('field', value, optional: stage_index)
% solve
ocp_solver.solve();
% get solution
utraj = ocp_solver.get('u');
xtraj = ocp_solver.get('x');
status = ocp_solver.get('status'); % 0 - success
ocp_solver.print('stat')
%% plots
ts = linspace(0, T, N+1);
figure; hold on;
states = {'xc', 'vc', 'pp', 'pc', 'xv', 'vv'};
for i=1:length(states)
subplot(length(states), 1, i);
plot(ts, xtraj(i,:)); grid on;
ylabel(states{i});
xlabel('t [s]')
end
when i run the ocp solver code, it returns status=1, means some NaN number in calculation.

I try to verify if my model is wrong, so i use ode45 to solve my model, and no problem.
ode45 solver code:
clear all; clc;
x0 = [0; 0; 5345000; 3000000; 0; 0];
tspan = [0 1];
u = [100; 10; 10];
m = 400;
Bp = 1024361;
F = 65637;
E1 = 1e9;
E2 = 1889610693;
Cv = 0.0018;
Lv = 0.016617;
Vp0 = 0.0263848;
Vc0 = 0.0018;
wv = 87;
ksi = 0.8;
kv = 0.000537;
A = 0.02356;
sys = @(t, x) [
x(2);
(A*x(4) + 10*m - Bp*x(2) - F)/m;
E1*((6.366e-7)*u(1)*u(2) - Cv*Lv*atan(u(3))*x(5)*sqrt(x(3)-x(4)))/Vp0;
E2*(Cv*Lv*atan(u(3))*x(5)*sqrt(x(3)-x(4)) - A*x(2))/(Vc0 + A*x(1));
x(6);
-(wv^2)*x(5) - 2*ksi*wv*x(6) + kv*(wv^2)*u(3)
];
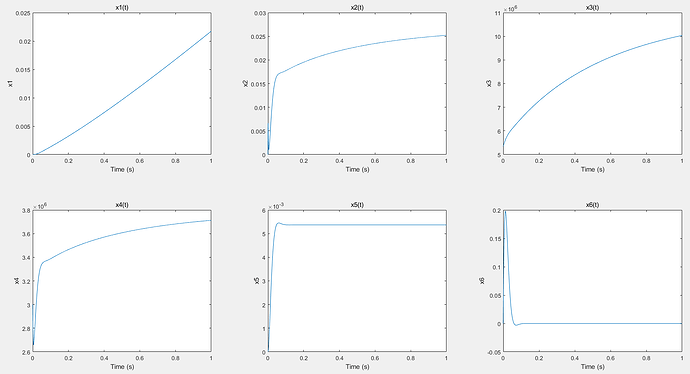
[t, x] = ode45(sys, tspan, x0);
figure;
subplot(2, 3, 1);
plot(t, x(:, 1)); title('x1(t)'); xlabel('Time (s)'); ylabel('x1');
subplot(2, 3, 2);
plot(t, x(:, 2)); title('x2(t)'); xlabel('Time (s)'); ylabel('x2');
subplot(2, 3, 3);
plot(t, x(:, 3)); title('x3(t)'); xlabel('Time (s)'); ylabel('x3');
subplot(2, 3, 4);
plot(t, x(:, 4)); title('x4(t)'); xlabel('Time (s)'); ylabel('x4');
subplot(2, 3, 5);
plot(t, x(:, 5)); title('x5(t)'); xlabel('Time (s)'); ylabel('x5');
subplot(2, 3, 6);
plot(t, x(:, 6)); title('x6(t)'); xlabel('Time (s)'); ylabel('x6');
ode45 solver result(look good):
based on the above, i want to know why ocp solver can’t work well. maybe i need to set parameter in a correct value, but there are so many parameter to set, i don’t know how to set. Thank you so much for seeing the end.
thanks in advance ![]()