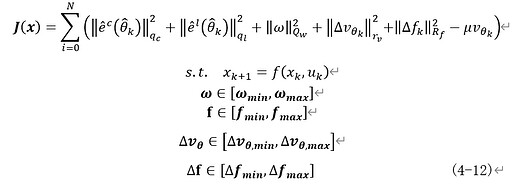Questions about "EXTERNAL" cost function

User Questions
1

Hi everyone! :wave:

I am writing an NMPC solver to solve nonlinear MPC problems using a Python interface. Since the cost function is not in a least squares (LS) form, I use the “EXTERNAL” type to define my cost function. However, I encounter some issues when setting up the solver.

Here is my model:

Code
    model_name = 'mpcc_ode'

    # parameters
    mass = 0.9 # [kg]
    g0 = 9.8015 # [m/s^2]
    arm_L = 0.16 # [m]
    cm = 4.888486266072161e-06
    ct = 0.000367717
    cq = cm/ct
    Ixx = 0.0046890742
    Iyy = 0.0046890742
    Izz = 0.010421166
    inv_Ixx = 1/Ixx
    inv_Iyy = 1/Iyy
    inv_Izz = 1/Izz
    M_PI = np.pi

    # set up states & controls
    p        = SX.sym('p', 3)
    v        = SX.sym('v', 3)
    q        = SX.sym('q', 4)
    w        = SX.sym('w', 3)
    f        = SX.sym('f', 4)
    theta    = SX.sym('theta')
    v_theta  = SX.sym('v_theta')
    x = vertcat(p, v, q, w, f, theta, v_theta)

    df       = SX.sym('df', 4)
    dv_theta = SX.sym('dv_theta')
    u = vertcat(df, dv_theta)

    # xdot
    p_dot       = SX.sym('p_dot', 3)
    v_dot       = SX.sym('v_dot', 3)
    q_dot       = SX.sym('q_dot', 4)
    w_dot       = SX.sym('w_dot', 3)
    f_dot       = SX.sym('f_dot', 4)
    theta_dot   = SX.sym('theta_dot')
    v_theta_dot = SX.sym('v_theta_dot')
    xdot = vertcat(p_dot, v_dot, q_dot, w_dot, f_dot, theta_dot, v_theta_dot)

    # dynamics
    f_expl = vertcat(v[0],
                     v[1],
                     v[2],
                     -2*(q[0]*q[2]+q[1]*q[3])*(f[0]+f[1]+f[2]+f[3])/mass,
                     -2*(q[2]*q[3]-q[0]*q[1])*(f[0]+f[1]+f[2]+f[3])/mass,
                     g0-(q[0]*q[0]-q[1]*q[1]-q[2]*q[2]+q[3]*q[3])*(f[0]+f[1]+f[2]+f[3])/mass,
                     0.5*(-q[1]*w[0]-q[2]*w[1]-q[3]*w[2]),
                     0.5*(q[0]*w[0]+q[2]*w[2]-q[3]*w[1]),
                     0.5*(q[0]*w[1]-q[1]*w[2]+q[3]*w[0]),
                     0.5*(q[0]*w[2]+q[1]*w[1]-q[2]*w[0]),
                     inv_Ixx*(Iyy-Izz)*w[1]*w[2]+inv_Ixx*arm_L*cos(M_PI/4)*(-f[0]+f[1]+f[2]-f[3]),
                     inv_Iyy*(Izz-Ixx)*w[0]*w[2]+inv_Iyy*arm_L*cos(M_PI/4)*(f[0]-f[1]+f[2]-f[3]),
                     inv_Izz*(Ixx-Iyy)*w[0]*w[1]+inv_Izz*cq*(f[0]+f[1]-f[2]-f[3]),
                     df[0],
                     df[1],
                     df[2],
                     df[3],
                     v_theta,
                     dv_theta
                    )

    f_impl = xdot - f_expl

    # algebraic variables
    z = []
    # parameters
    p = []

    model = AcadosModel()

    model.f_impl_expr = f_impl
    model.f_expl_expr = f_expl
    model.x = x
    model.xdot = xdot
    model.u = u
    model.z = z
    model.p = p
    model.name = model_name

The cost function is given by:

cgi-bin_mmwebwx-bin_webwxgetmsgimg_&MsgID=732181387056331818&skey=@crypt_c3fc4412_438d9524db22c010e951d8b4a9d09cff&mmweb_appid=wx_webfilehelper
cgi-bin_mmwebwx-bin_webwxgetmsgimg_&MsgID=732181387056331818&skey=@crypt_c3fc4412_438d9524db22c010e951d8b4a9d09cff&mmweb_appid=wx_webfilehelper828×300 44.2 KB

First question:

In this cost function, the value q_c is a dynamic parameter, meaning that I need to change it each time I use this solver to solve an optimization problem.

To modify q_c , I set it as a dynamic parameter while keeping other cost weights fixed using the following code:

Code
        # set dynamic cost weight q_c
        self.cost_error_contour_param = ca.SX.sym('cost_error_contour')
        self.ocp.model.p = ca.vertcat(self.cost_error_contour_param)
        self.ocp.dims.np = 1
        self.ocp.parameter_values = np.array([500])

Then, I define part of the q_c cost function as:

Code
        p_x, p_y, p_z = self.model.x[0], self.model.x[1], self.model.x[2]
        theta = self.model.x[-2]

        p_theta_x_ref = 0.57735 * theta
        p_theta_y_ref = 0.57735 * theta
        p_theta_z_ref = 0.57735 * theta

        error_pos_x = p_x - p_theta_x_ref
        error_pos_y = p_y - p_theta_y_ref
        error_pos_z = p_z - p_theta_z_ref

        v_theta_x_ref = 0.57735
        v_theta_y_ref = 0.57735
        v_theta_z_ref = 0.57735

        self.ocp.cost.cost_type = "EXTERNAL"
        self.ocp.cost.cost_type_e = "EXTERNAL"

        error_contour_x = (1 - v_theta_x_ref**2) * error_pos_x - (v_theta_x_ref * v_theta_y_ref) * error_pos_y - (v_theta_x_ref * v_theta_z_ref) * error_pos_z
        error_contour_y = (1 - v_theta_y_ref**2) * error_pos_y - (v_theta_y_ref * v_theta_x_ref) * error_pos_x - (v_theta_y_ref * v_theta_z_ref) * error_pos_z
        error_contour_z = (1 - v_theta_z_ref**2) * error_pos_z - (v_theta_x_ref * v_theta_z_ref) * error_pos_x - (v_theta_y_ref * v_theta_z_ref) * error_pos_y

        cost_error_contour = ca.sum2(self.ocp.model.p[0] * error_contour_x 
                                + self.ocp.model.p[0] * error_contour_y 
                                + self.ocp.model.p[0] * error_contour_z)

Other cost functions are omitted here. The final cost function is:

Code
        cost_expr = cost_error_lag + cost_error_contour + cost_error_w + cost_error_df + cost_error_dv_theta + cost_error_v
        self.ocp.model.cost_expr_ext_cost = ca.sum2(cost_expr)
        self.ocp.model.cost_expr_ext_cost_e = ca.SX(0)
        self.acados_solver = AcadosOcpSolver(self.ocp, json_file = 'acados_ocp.json')

However, when I use acados_solver in the main function to solve the NMPC problem, I attempt to modify self.ocp.model.p[0] using:

Code
    # Init solver
    mpcc_controller = MPCC_Controller()

    # change q_c
    mpcc_controller.acados_solver.set(0, "p", 200.0)

    # solve NMPC question
    _dt, w = mpcc_controller.mpcc_control(current_state)

It seems that the solution does not update when I modify self.ocp.model.p[0] using mpcc_controller.acados_solver.set(0, "p", 200.0), even when I change the value to 0.0 or 5000.0. However, if I modify the value in self.ocp.parameter_values = np.array([500]), the solution changes.

Are there any errors in my code, or is there another way to correctly modify this parameter? Should I consider using the “NONLINEAR_LS” cost function instead?

Second question:

Another question is that variable \hat{e}^{l}\left(\hat{\theta}_{k}\right) in the cost function is computed as

\hat{e}^{l}\left(\hat{\theta}_{k}\right) = p_x\cdot p\left ( {\theta}_{k} \right )_x + p_y\cdot p\left ( {\theta}_{k} \right )_y +p_z\cdot p\left ( {\theta}_{k} \right )_z

where p_x, p_y, p_z and \theta_k are state variables in this NMPC question, p\left ( {\theta}_{k} \right )_x , p\left ( {\theta}_{k} \right )_y and p\left ( {\theta}_{k} \right )_z can be calculated by:

p\left ( {\theta}_{k} \right )_x = a_{0,x} + a_{1,x} \cdot {\theta}_{k} + a_{2,x} \cdot {\theta}_{k}^2 + a_{3,x} \cdot {\theta}_{k}^3
p\left ( {\theta}_{k} \right )_y = a_{0,y} + a_{1,y} \cdot {\theta}_{k} + a_{2,y} \cdot {\theta}_{k}^2 + a_{3,y} \cdot {\theta}_{k}^3
p\left ( {\theta}_{k} \right )_z= a_{0,z} + a_{1,z} \cdot {\theta}_{k} + a_{2,z} \cdot {\theta}_{k}^2 + a_{3,z} \cdot {\theta}_{k}^3

The polynomial coefficients a_{i,*} are dynamically updated.

Similarly, I encounter the same issue when trying to dynamically modify these 12 coefficients. Additionally, if the prediction step size is 20, the first 10 steps share one set of polynomial coefficients, while the last 10 steps have a different set. How can I set these coefficients properly when creating the solver?

Total Python Codes Here:

mpcc_ocp.py:

Code

from acados_template import AcadosOcp, AcadosOcpSolver
from mpcc_model import export_mpcc_ode_model
import numpy as np
import casadi as ca
import scipy.linalg
from os.path import dirname, join, abspath
import time


class MPCC_Controller:
    def __init__(self, cost_params=None):
        self.ocp = AcadosOcp()       # OCP 
        self.model = export_mpcc_ode_model()
        self.ocp.model = self.model  # model set

        # parameters

        default_cost_params = {
            'cost_error_lag': 1000.0,
            'cost_error_w': 1.0,
            'cost_error_df': 1.0,
            'cost_error_dv_theta': 10.0,
            'cost_error_v': 500.0,
            'N': 21,
            'Tf': 1.05
        }
        self.cost_params = {**default_cost_params, **(cost_params or {})}

        # set dynamic q_c
        self.cost_error_contour_param = ca.SX.sym('cost_error_contour')
        self.ocp.model.p = ca.vertcat(self.cost_error_contour_param)
        self.ocp.dims.np = 1
        self.ocp.parameter_values = np.array([500.0])

        self.nx = self.model.x.size()[0]    # dimension of state
        self.nu = self.model.u.size()[0]    # dimension of control
        self.ny = self.nx + self.nu         # dimension of control + state
        self.ny_e = self.nx                 # end dimension of control + state

        # prediction steps and total prediction time
        self.ocp.solver_options.N_horizon = self.cost_params['N']
        self.ocp.dims.N = self.cost_params['N']
        self.ocp.solver_options.tf = self.cost_params['Tf']

    

        p_x, p_y, p_z = self.model.x[0], self.model.x[1], self.model.x[2]
        theta = self.model.x[-2]

        p_theta_x_ref = 0.57735 * theta
        p_theta_y_ref = 0.57735 * theta
        p_theta_z_ref = 0.57735 * theta

        error_pos_x = p_x - p_theta_x_ref
        error_pos_y = p_y - p_theta_y_ref
        error_pos_z = p_z - p_theta_z_ref

        v_theta_x_ref = 0.57735
        v_theta_y_ref = 0.57735
        v_theta_z_ref = 0.57735

        self.ocp.cost.cost_type = "EXTERNAL"
        self.ocp.cost.cost_type_e = "EXTERNAL"

        # cost function for q_l
        cost_error_lag = self.cost_params['cost_error_lag'] * (ca.dot(v_theta_x_ref, error_pos_x) + ca.dot(v_theta_y_ref, error_pos_y) + ca.dot(v_theta_z_ref, error_pos_z))
        print(f"cost_error_lag shape: {cost_error_lag.shape}")

        error_contour_x = (1 - v_theta_x_ref**2) * error_pos_x - (v_theta_x_ref * v_theta_y_ref) * error_pos_y - (v_theta_x_ref * v_theta_z_ref) * error_pos_z
        error_contour_y = (1 - v_theta_y_ref**2) * error_pos_y - (v_theta_y_ref * v_theta_x_ref) * error_pos_x - (v_theta_y_ref * v_theta_z_ref) * error_pos_z
        error_contour_z = (1 - v_theta_z_ref**2) * error_pos_z - (v_theta_x_ref * v_theta_z_ref) * error_pos_x - (v_theta_y_ref * v_theta_z_ref) * error_pos_y
        print(f"error_contour_x shape: {error_contour_x.shape}")

        error_w_x = self.model.x[10]**2
        error_w_y = self.model.x[11]**2
        error_w_z = self.model.x[12]**2
        print(f"error_w_x shape: {error_w_x.shape}")

        error_df_0 = self.model.u[0]**2
        error_df_1 = self.model.u[1]**2
        error_df_2 = self.model.u[2]**2
        error_df_3 = self.model.u[3]**2
        print(f"error_df_0 shape: {error_df_0.shape}")

        error_dv_theta = self.model.u[4]**2
        print(f"error_dv_theta shape: {error_dv_theta.shape}")

        error_v = self.model.x[13]**2
        print(f"error_v shape: {error_v.shape}")

        # cost function for q_c
        cost_error_contour = ca.sum2(self.ocp.model.p[0] * error_contour_x 
                                + self.ocp.model.p[0] * error_contour_y 
                                + self.ocp.model.p[0] * error_contour_z)
        print(f"cost_error_contour shape: {cost_error_contour.shape}")

        # cost function for q_w
        cost_error_w = ca.sum2(self.cost_params['cost_error_w'] * error_w_x 
                              + self.cost_params['cost_error_w'] * error_w_y 
                              + self.cost_params['cost_error_w'] * error_w_z)
        print(f"cost_error_w shape: {cost_error_w.shape}")

        # cost function for R_df
        cost_error_df = ca.sum2(self.cost_params['cost_error_df'] * error_df_0
                               + self.cost_params['cost_error_df'] * error_df_1
                               + self.cost_params['cost_error_df'] * error_df_2
                               + self.cost_params['cost_error_df'] * error_df_3)
        print(f"cost_error_df shape: {cost_error_df.shape}")

        # cost function for R_dv_theta
        cost_error_dv_theta = ca.sum2(self.cost_params['cost_error_dv_theta'] * error_dv_theta)
        print(f"cost_error_dv_theta shape: {cost_error_dv_theta.shape}")

        # cost function for R_v
        cost_error_v = ca.sum2(self.cost_params['cost_error_v'] * error_v)
        print(f"cost_error_v shape: {cost_error_v.shape}")

        # total cost function
        cost_expr = cost_error_lag + cost_error_contour + cost_error_w + cost_error_df + cost_error_dv_theta + cost_error_v
        print(f"cost_expr type: {type(cost_expr)}, shape: {cost_expr.shape}")

        # set cost function and end cost function
        self.ocp.model.cost_expr_ext_cost = ca.sum2(cost_expr)
        self.ocp.model.cost_expr_ext_cost_e = ca.SX(0)

        # set constraints
        self.ocp.constraints.lbu = np.array([-20, -20, -20, -20, 0]) 
        self.ocp.constraints.ubu = np.array([20, 20, 20, 20, 50])
        self.ocp.constraints.x0  = np.array([0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0])  # 初始状态
        self.ocp.constraints.idxbu = np.array([0, 1, 2, 3, 4]) 

        self.ocp.constraints.lbx = np.array([-3.14, -3.14, -3.14, 0.01, 0.01, 0.01, 0.01, 0]) 
        self.ocp.constraints.ubx = np.array([3.14, 3.14, 3.14, 20, 20, 20, 20, 20]) 
        self.ocp.constraints.idxbx = np.array([10, 11, 12, 13, 14, 15, 16, 18]) 

        self.ocp.constraints.x0  = np.array([0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0])  # 初始状态

        # set solver parameters

        # self.ocp.solver_options.qp_solver = 'FULL_CONDENSING_QPOASES'
        self.ocp.solver_options.qp_solver = 'FULL_CONDENSING_HPIPM'  
        # self.ocp.solver_options.qp_solver = 'PARTIAL_CONDENSING_HPIPM'  
        self.ocp.solver_options.hessian_approx = 'EXACT'
        self.ocp.solver_options.integrator_type = 'ERK'
        self.ocp.solver_options.qp_solver_iter_max = 5000
        self.ocp.solver_options.print_level = 0
        self.ocp.solver_options.nlp_solver_type = 'SQP_RTI'

        # create ocp solver
        self.acados_solver = AcadosOcpSolver(self.ocp, json_file = 'acados_ocp.json')
        self.acados_solver.set(0, "p", np.array([self.ocp.parameter_values[0]]))

        print("NMPC Controller Init Done")

    def mpcc_control(self, current_state):
        _start = time.perf_counter()
        # set initial state
        self.acados_solver.set(0, 'lbx', current_state)
        self.acados_solver.set(0, 'ubx', current_state)

        # solve the optimization problem
        self.acados_solver.solve()
        
        # print the solution
        w_opt_acados = np.ndarray((self.cost_params['N'], 5))  # input
        x_opt_acados = np.ndarray((self.cost_params['N'] + 1, len(current_state)))   # state
        x_opt_acados[0, :] = self.acados_solver.get(0, "x")
        for i in range(self.cost_params['N']):
            w_opt_acados[i, :] = self.acados_solver.get(i, "u")
            x_opt_acados[i + 1, :] = self.acados_solver.get(i + 1, "x")
        # return w_opt_acados, x_opt_acados
        _end = time.perf_counter()
        _dt = (_end - _start) * 1000  # change time to ms
        print(f"Time taken to run mpcc_control: {_dt:.3f} ms")
        return _dt, w_opt_acados[0]  # return the first control input

    def update_cost_countor_params(self, new_cost_error_contour):
        """
        change cost_error_contour
        """
        self.acados_solver.set(0, "p", np.array([new_cost_error_contour]))

if __name__ == '__main__':
    print("ACADOS MPCC TEST")

    # solver init
    mpcc_controller = MPCC_Controller()
    print(mpcc_controller.acados_solver.get(0, "p")[0]) 

    # set initial state
    current_state = np.array([0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0])

    # change q_c
    mpcc_controller.acados_solver.reset()
    mpcc_controller.acados_solver.set(0, "p", 500.0)
    print(mpcc_controller.acados_solver.get(0, "p")[0]) 

    # solve the optimization problem
    _dt, w = mpcc_controller.mpcc_control(current_state)
    print("Control Input:")
    print(w)

mpcc_model.py:

Code

from acados_template import AcadosModel
from casadi import SX, vertcat, sin, cos
import numpy as np

def export_mpcc_ode_model():

    model_name = 'mpcc_ode'

    # parameters
    mass = 0.9 # [kg]
    g0 = 9.8015 # [m/s^2]
    arm_L = 0.16 # [m]
    cm = 4.888486266072161e-06
    ct = 0.000367717
    cq = cm/ct
    Ixx = 0.0046890742
    Iyy = 0.0046890742
    Izz = 0.010421166
    inv_Ixx = 1/Ixx
    inv_Iyy = 1/Iyy
    inv_Izz = 1/Izz
    M_PI = np.pi

    # set up states & controls
    p        = SX.sym('p', 3)
    v        = SX.sym('v', 3)
    q        = SX.sym('q', 4)
    w        = SX.sym('w', 3)
    f        = SX.sym('f', 4)
    theta    = SX.sym('theta')
    v_theta  = SX.sym('v_theta')
    x = vertcat(p, v, q, w, f, theta, v_theta)

    df       = SX.sym('df', 4)
    dv_theta = SX.sym('dv_theta')
    u = vertcat(df, dv_theta)

    # xdot
    p_dot       = SX.sym('p_dot', 3)
    v_dot       = SX.sym('v_dot', 3)
    q_dot       = SX.sym('q_dot', 4)
    w_dot       = SX.sym('w_dot', 3)
    f_dot       = SX.sym('f_dot', 4)
    theta_dot   = SX.sym('theta_dot')
    v_theta_dot = SX.sym('v_theta_dot')
    xdot = vertcat(p_dot, v_dot, q_dot, w_dot, f_dot, theta_dot, v_theta_dot)

    # dynamics
    f_expl = vertcat(v[0],
                     v[1],
                     v[2],
                     -2*(q[0]*q[2]+q[1]*q[3])*(f[0]+f[1]+f[2]+f[3])/mass,
                     -2*(q[2]*q[3]-q[0]*q[1])*(f[0]+f[1]+f[2]+f[3])/mass,
                     g0-(q[0]*q[0]-q[1]*q[1]-q[2]*q[2]+q[3]*q[3])*(f[0]+f[1]+f[2]+f[3])/mass,
                     0.5*(-q[1]*w[0]-q[2]*w[1]-q[3]*w[2]),
                     0.5*(q[0]*w[0]+q[2]*w[2]-q[3]*w[1]),
                     0.5*(q[0]*w[1]-q[1]*w[2]+q[3]*w[0]),
                     0.5*(q[0]*w[2]+q[1]*w[1]-q[2]*w[0]),
                     inv_Ixx*(Iyy-Izz)*w[1]*w[2]+inv_Ixx*arm_L*cos(M_PI/4)*(-f[0]+f[1]+f[2]-f[3]),
                     inv_Iyy*(Izz-Ixx)*w[0]*w[2]+inv_Iyy*arm_L*cos(M_PI/4)*(f[0]-f[1]+f[2]-f[3]),
                     inv_Izz*(Ixx-Iyy)*w[0]*w[1]+inv_Izz*cq*(f[0]+f[1]-f[2]-f[3]),
                     df[0],
                     df[1],
                     df[2],
                     df[3],
                     v_theta,
                     dv_theta
                    )

    f_impl = xdot - f_expl

    # algebraic variables
    z = []
    # parameters
    p = []

    model = AcadosModel()

    model.f_impl_expr = f_impl
    model.f_expl_expr = f_expl
    model.x = x
    model.xdot = xdot
    model.u = u
    model.z = z
    model.p = p
    model.name = model_name

    # store meta information
    model.x_labels = ['$p$ [m]', '$v$ [m/s]', '$q$', '$w$ [rad/s]', '$f$ [N]', '$\theta$ [m]', '$v_{\theta}$ [m/s]']
    model.u_labels = ['$df$ [F/s]', '$dv_{\theta}$ [m/s^2]']
    model.t_label = '$t$ [s]'

    return model

Thanks for your advice! :slight_smile:

2

Hi :waving_hand:

in general, your approach is correct. You need to put all CasADi symbolics of your parameters in model.p. The values in ocp.parameter_values define the initial value of the parameters for each stage. After solver creation you can update these parameters any time using solver.set(stage, "p", new_values). Note that the parameters might be different for each stage, i.e. you need to set them for all stages 0, …, N. You can get the current parameter values with solver.get(stage, "p").

Note that you do not need to set any of the dimensions in ocp.dims as they will be detected when creating the solver.

Hope this helps!
Katrin

3

And one more remark regarding your cost function: I would recommend to use the convex-over-nonlinear cost module of acados. For the linear term in your cost, the outer convex function would just be the identity.

With this cost module, you can use the GAUSS_NEWTON option which corresponds to a Generalizes Gauss-Newton Hessian approximation in this case and is guaranteed to be positive semi-definite.

4

Thank you for your detailed explanation! :smiling_face_with_three_hearts: Now I understand that I need to set the parameters for all stages individually using solver.set(stage, "p", new_values). Your clarification really helped me figure out the issue. I appreciate your support! :grinning_face: