Penalties and Constraints for control input rates via Augmented States

User Questions
1

Hello everyone!

I’m new to acados and currently I want to implement penalties and constraints on the control input rate. I read similar questions in the forum, and the feasible way is to implement it through augmented state variables. But when I tried it, the effect was not satisfactory. It can only operate correctly when there is a certain proportion of weight values (currently only one set of weight parameters), but its tracking effect is not good. The result is as follows:

737×577 33.7 KB

Among them, u is the original control input, which is added to the dynamic model in the form of augmented state variables.

What details should I pay attention to here? :grinning:

Best regards,
AnLan.

2

Can someone answer it? thank! :sob:

3

Hi,

I think it should be just a matter of tuning.
Also, you will need a long enough control horizon and ideally a terminal cost.

I think it would be nice to have an example with control rates in acados.
Maybe you can contribute one.
It is hard to say what is the problem in your particular case without having the code.

Best,
Jonathan

4

Hello, FreyJo. Thank you for your reply.

I’ll sort out the code and post it. The weight parameters cannot be adjusted flexibly when using augmented state variables, which is not clear to me why.

5

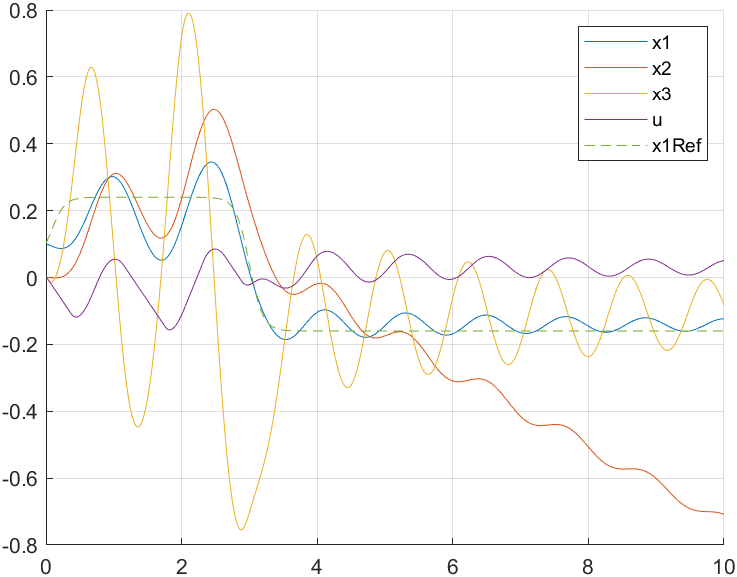
Here’s the original code:
F8_crusader_model

function model = F8_crusader_model()
import casadi.*

%% System dimension
nx = 3;
nu = 1;

%% System parameters
a1 = -0.877; a2 = -0.088; a3 = 0.47; a4 = -0.019; a5 = 3.846; a6 = -0.215;
a7 = 0.28; a8 = 0.47; a9 = 0.63;
c1 = -4.208; c2 = -0.396; c3 = -0.47; c4 = -3.564; c5 = -20.967; c6 = 6.265;
c7 = 46; c8 = 61.1;

%% Symbolic variables
% states
x1 = SX.sym('x1');
x2 = SX.sym('x2');
x3 = SX.sym('x3');
sym_x = vertcat(x1, x2, x3);

% controls
u = SX.sym('u');
sym_u = u;

% state derivatives
sym_xdot = SX.sym('xdot', nx, 1); 

%% The system dynamics
% Explicit Dynamics
expr_f_expl = vertcat(a1*x1+x3+a2*x1*x3+a3*x1.^2+a4*x2.^2-x1.^2*x3+a5*x1.^3+a6*u+a7*x1.^2*u+a8*x1*u.^2+a9*u.^3, ...
                      x3, ...
                      c1*x1+c2*x3+c3*x1.^2+c4*x1.^3+c5*u+c6*x1.^2*u+c7*x1*u.^2+c8*u.^3);

% Implicit Dynamics
expr_f_impl = expr_f_expl - sym_xdot;

% Discrete Dynamics

%% fill structure
model.nx = nx;
model.nu = nu;
model.sym_x = sym_x;
model.sym_u = sym_u;
model.sym_xdot = sym_xdot;
model.expr_f_expl = expr_f_expl;
model.expr_f_impl = expr_f_impl;

end

F8_crusader_ocp

%% Test of native matlab interface
clear; close all; clc;

% run acados_env_variables_windows.m
run('../acados_env_variables_windows.m');

% check that env.sh has been run
env_run = getenv('ENV_RUN');
if (~strcmp(env_run, 'true'))
	error('env.sh has not been sourced! Before executing this example, run: source env.sh');
end

%% Solver options
% Code generation
compile_interface = 'false';
codgen_model = 'false';
compile_model = 'false';
output_dir = 'build';

% Shooting nodes
param_scheme_N = 10;                     % horizon parameter (need T)

% Integrator
sim_method = 'erk';
sim_method_num_stages = 4;
sim_method_num_steps = 1;
% sim_method_newton_iter = 3;            % for 'irk' 'irk_gnsf'
gnsf_detect_struct = 'true';

% NLP solver
nlp_solver = 'sqp_rti';
nlp_solver_max_iter = 100;
nlp_solver_tol_stat = 10e-6;
nlp_solver_tol_eq = 10e-6;
nlp_solver_tol_ineq = 10e-6;
nlp_solver_tol_comp = 10e-6;
nlp_solver_ext_qp_res = 0;               % for debugging
nlp_solver_step_length = 1.0;
rti_phase = 0;                           % for sqp_rti

% QP solver
qp_solver = 'partial_condensing_hpipm';
qp_solver_iter_max = 50;
qp_solver_cond_N = 5;                    % for partial_condensing
qp_solver_cond_ric_alg = 1;
qp_solver_ric_alg = 1;                   % for HPIPM
qp_solver_warm_start = 0;
% warm_start_first_qp = 1;

% Globalization
globalization = 'fixed_step';
% alpha_min = 0.05;                      % for merit_backtracking 
% alpha_reduction = 0.7;

% Hessian approximation
nlp_solver_exact_hessian = 'false';      % 'gauss newton'
regularize_method = 'no_regularize';
levenberg_marquardt = 0.0;
% exact_hess_dyn = 1;                    % for exact_hessian = 'true'
% exact_hess_cost = 1;
% exact_hess_constr = 1;

% Other
print_level = 0;

%% OCP options

% model_name = 'F8_crusader';

% CasADi expression
model = F8_crusader_model;

% time horizon length
h = 0.01;
T = param_scheme_N*h;

% dimension
nx = model.nx;
nu = model.nu;
ny = nx + nu;                  % number of outputs in lagrange term
ny_e = nx;                     % number of outputs in mayer term
nbx = nx;                      % number of state bounds
nbu = nu;                      % number of input bounds

% cost
cost_type = 'linear_ls';
cost_type_e = 'linear_ls';
Vx = zeros(ny,nx); Vx(1:nx,:) = eye(nx);        % state-to-output matrix in lagrange term
Vu = zeros(ny,nu); Vu(nx+1:ny,:) = eye(nu);     % input-to-output matrix in lagrange term
Vx_e = zeros(ny_e,nx); Vx_e(1:nx,:) = eye(nx);  % state-to-output matrix in mayer term
W = diag([25*2, 0, 0, 0.05*2]);
W_e = W(1:ny_e,1:ny_e);
y_ref = zeros(ny,1);                            % set intial references
y_ref_e = zeros(ny_e,1);

% constraint
constr_type = 'bgh';
dyn_type = 'explicit';
x0 = [0.1; 0; 0];
Jbx = eye(nbx,nx);
lbx = [-0.2; -1; -1];
ubx = [0.4; 1; 1];
Jbu = eye(nbu,nu);
lbu = -0.3;
ubu = 0.5;

%% acados ocp model
ocp_model = acados_ocp_model();
% ocp_model.set('name', model_name);

% end time
ocp_model.set('T', T);

% symbolics
ocp_model.set('sym_x', model.sym_x);
ocp_model.set('sym_u', model.sym_u);
ocp_model.set('sym_xdot', model.sym_xdot);

% cost
ocp_model.set('cost_type', cost_type);
ocp_model.set('cost_type_e', cost_type_e);
ocp_model.set('cost_Vx', Vx);
ocp_model.set('cost_Vu', Vu);
ocp_model.set('cost_Vx_e', Vx_e);
ocp_model.set('cost_W', W);
ocp_model.set('cost_W_e', W_e);
ocp_model.set('cost_y_ref', y_ref);
ocp_model.set('cost_y_ref_e', y_ref_e);

% constraint
ocp_model.set('dyn_type', dyn_type);            
ocp_model.set('dyn_expr_f', model.expr_f_expl); 
ocp_model.set('constr_x0', x0);                 % dynamic
ocp_model.set('constr_type', constr_type);
ocp_model.set('constr_Jbx', Jbx);
ocp_model.set('constr_lbx', lbx);
ocp_model.set('constr_ubx', ubx);
ocp_model.set('constr_Jbu', Jbu);
ocp_model.set('constr_lbu', lbu);
ocp_model.set('constr_ubu', ubu);

disp('ocp_model.model_struct: ')
disp(ocp_model.model_struct)

%% acados ocp opts
ocp_opts = acados_ocp_opts();

% Code generation
ocp_opts.set('compile_interface', compile_interface);
ocp_opts.set('codgen_model', codgen_model);
ocp_opts.set('compile_model', compile_model);
ocp_opts.set('output_dir', output_dir);

% Shooting nodes
ocp_opts.set('param_scheme_N', param_scheme_N);

% Integrator
ocp_opts.set('sim_method', sim_method);
ocp_opts.set('sim_method_num_stages', sim_method_num_stages);
ocp_opts.set('sim_method_num_steps', sim_method_num_steps);
% ocp_opts.set('sim_method_newton_iter', sim_method_newton_iter);
ocp_opts.set('gnsf_detect_struct', gnsf_detect_struct);

% NLP solver
ocp_opts.set('nlp_solver', nlp_solver);
ocp_opts.set('qp_solver_iter_max', qp_solver_iter_max);
ocp_opts.set('nlp_solver_tol_stat', nlp_solver_tol_stat);
ocp_opts.set('nlp_solver_tol_eq', nlp_solver_tol_eq);
ocp_opts.set('nlp_solver_tol_ineq', nlp_solver_tol_ineq);
ocp_opts.set('nlp_solver_tol_comp', nlp_solver_tol_comp);
ocp_opts.set('nlp_solver_ext_qp_res', nlp_solver_ext_qp_res);
ocp_opts.set('nlp_solver_step_length', nlp_solver_step_length);
ocp_opts.set('rti_phase', rti_phase);

% QP solver
ocp_opts.set('qp_solver', qp_solver);
ocp_opts.set('qp_solver_iter_max', qp_solver_iter_max);
ocp_opts.set('qp_solver_cond_N', qp_solver_cond_N);
ocp_opts.set('qp_solver_cond_ric_alg', qp_solver_cond_ric_alg);
ocp_opts.set('qp_solver_ric_alg', qp_solver_ric_alg);
ocp_opts.set('qp_solver_warm_start', qp_solver_warm_start);
% ocp_opts.set('nlp_solver_warm_start_first_qp', warm_start_first_qp);

% Globalization
ocp_opts.set('globalization', globalization);
% ocp_opts.set('alpha_min', alpha_min);
% ocp_opts.set('alpha_reduction', alpha_reduction);

% Hessian approximation
ocp_opts.set('nlp_solver_exact_hessian', nlp_solver_exact_hessian);
ocp_opts.set('regularize_method', regularize_method);
ocp_opts.set('levenberg_marquardt', levenberg_marquardt);
% ocp_opts.set('exact_hess_dyn', exact_hess_dyn);
% ocp_opts.set('exact_hess_cost', exact_hess_cost);
% ocp_opts.set('exact_hess_constr', exact_hess_constr);

% Other
ocp_opts.set('print_level', print_level);

disp('ocp_opts.opts_struct: ');
disp(ocp_opts.opts_struct);

%% create ocp solver
ocp = acados_ocp(ocp_model, ocp_opts);

%% Simulation
Duration = 10;
N_sim = Duration/h;

% initialize data structs
x_sim = zeros(nx, N_sim+1);
u_sim = zeros(nu, N_sim+1);
cost_sim = zeros(1, N_sim+1);
x_sim(:, 1) = x0;
u_sim(:, 1) = zeros(nu, 1);
cost_sim(1, 1) = 0;

% set trajectory initialization (also can use plant: create acados integrator)
ocp.set('init_x', x0 * ones(1,param_scheme_N+1));
% ocp.set('init_x', zeros(nx,param_scheme_N+1));
ocp.set('init_u', zeros(nu, param_scheme_N));

% time-varying reference trajectory
x1ref_FUN = @(t) 0.4.*(-(0.5./(1+exp(t./0.1-0.8))) + (1./(1+exp(t./0.1-30))) - 0.4);
t = 0:h:Duration;
x1ref = 0.4.*(-(0.5./(1+exp(t./0.1-0.8))) + (1./(1+exp(t./0.1-30))) - 0.4);

% run mpc
fprintf('Simulation started.  It might take a while...\n')
tic;
for i = 1:N_sim

    % update reference
    t_ref = (i-1:i+param_scheme_N).*h;
    x1_ref = x1ref_FUN(t_ref);
    for j = 0:param_scheme_N-1
        y_ref(1) = x1_ref(j+1);
        ocp.set('cost_y_ref', y_ref, j);
    end
    y_ref_e(1) = x1_ref(param_scheme_N+1);
    ocp.set('cost_y_ref_e', y_ref_e, param_scheme_N);

    % solve ocp
    ocp.solve();
    status = ocp.get('status');      % 0 - success
    if status ~= 0
        error(sprintf('acados returned status %d in closed loop iteration %d. Exiting.', status, i));
    end

    % get solution t0
    x0 = ocp.get('x', 0);
    u0 = ocp.get('u', 0);
    x_sim(:, i+1) = x0;
    u_sim(:, i+1) = u0;
    cost_sim(1, i+1) = ocp.get_cost();

    % update initial state
    x0 = ocp.get('x', 1);
    ocp.set('constr_x0', x0);
    
end
tElapsed = toc
fprintf('Simulation finished!\n')

%% Plot
figure; hold on; grid on;
plot(t, x_sim, t, x1ref, '--');
legend('x1', 'x2', 'x3', 'x1Ref');

figure; hold on; grid on;
plot(t, u_sim);
legend('the control input');

figure; hold on; grid on;
plot(t, cost_sim);
legend('the cost curve');

%% go embedded to generate templated C code
% ocp.generate_c_code;

Here’s the code using augmented state variables:
F8_crusader_model

function model = F8_crusader_model()
import casadi.*

%% System dimension
nx = 4;
nu = 1;

%% System parameters
a1 = -0.877; a2 = -0.088; a3 = 0.47; a4 = -0.019; a5 = 3.846; a6 = -0.215;
a7 = 0.28; a8 = 0.47; a9 = 0.63;
c1 = -4.208; c2 = -0.396; c3 = -0.47; c4 = -3.564; c5 = -20.967; c6 = 6.265;
c7 = 46; c8 = 61.1;

%% Symbolic variables
% states
x1 = SX.sym('x1');
x2 = SX.sym('x2');
x3 = SX.sym('x3');
x4 = SX.sym('x4');
sym_x = vertcat(x1, x2, x3, x4);

% controls
u = SX.sym('u');
sym_u = u;

% state derivatives
sym_xdot = SX.sym('xdot', nx, 1); 

%% The system dynamics
% Explicit Dynamics
expr_f_expl = vertcat(a1*x1+x3+a2*x1*x3+a3*x1.^2+a4*x2.^2-x1.^2*x3+a5*x1.^3+a6*x4+a7*x1.^2*x4+a8*x1*x4.^2+a9*x4.^3, ...
                      x3, ...
                      c1*x1+c2*x3+c3*x1.^2+c4*x1.^3+c5*x4+c6*x1.^2*x4+c7*x1*x4.^2+c8*x4.^3, ...
                      u);

% Implicit Dynamics
expr_f_impl = expr_f_expl - sym_xdot;

% Discrete Dynamics

%% fill structure
model.nx = nx;
model.nu = nu;
model.sym_x = sym_x;
model.sym_u = sym_u;
model.sym_xdot = sym_xdot;
model.expr_f_expl = expr_f_expl;
model.expr_f_impl = expr_f_impl;

end

F8_crusader_ocp

%% Test of native matlab interface
clear; close all; clc;

% run acados_env_variables_windows.m
run('../acados_env_variables_windows.m');

% check that env.sh has been run
env_run = getenv('ENV_RUN');
if (~strcmp(env_run, 'true'))
	error('env.sh has not been sourced! Before executing this example, run: source env.sh');
end

%% Solver options
% Code generation
compile_interface = 'false';
codgen_model = 'false';
compile_model = 'false';
output_dir = 'build';

% Shooting nodes
param_scheme_N = 10;                     % horizon parameter (need T)

% Integrator
sim_method = 'erk';
sim_method_num_stages = 4;
sim_method_num_steps = 1;
% sim_method_newton_iter = 3;            % for 'irk' 'irk_gnsf'
gnsf_detect_struct = 'true';

% NLP solver
nlp_solver = 'sqp_rti';
nlp_solver_max_iter = 100;
nlp_solver_tol_stat = 10e-6;
nlp_solver_tol_eq = 10e-6;
nlp_solver_tol_ineq = 10e-6;
nlp_solver_tol_comp = 10e-6;
nlp_solver_ext_qp_res = 0;               % for debugging
nlp_solver_step_length = 1.0;
rti_phase = 0;                           % for sqp_rti

% QP solver
qp_solver = 'partial_condensing_hpipm';
qp_solver_iter_max = 50;
qp_solver_cond_N = 5;                    % for partial_condensing
qp_solver_cond_ric_alg = 1;
qp_solver_ric_alg = 1;                   % for HPIPM
qp_solver_warm_start = 1;
% warm_start_first_qp = 1;

% Globalization
globalization = 'fixed_step';
% alpha_min = 0.05;                      % for merit_backtracking 
% alpha_reduction = 0.7;

% Hessian approximation
nlp_solver_exact_hessian = 'false';      % 'gauss newton'
regularize_method = 'no_regularize';
levenberg_marquardt = 0.0;
% exact_hess_dyn = 1;                    % for exact_hessian = 'true'
% exact_hess_cost = 1;
% exact_hess_constr = 1;

% Other
print_level = 0;

%% OCP options

% model_name = 'F8_crusader';

% CasADi expression
model = F8_crusader_model;

% time horizon length
h = 0.01;
T = param_scheme_N*h;

% dimension
nx = model.nx;
nu = model.nu;
ny = nx + nu;                  % number of outputs in lagrange term
ny_e = nx;                     % number of outputs in mayer term
nbx = nx;                      % number of state bounds
nbu = nu;                      % number of input bounds

% cost
cost_type = 'linear_ls';
cost_type_e = 'linear_ls';
Vx = zeros(ny,nx); Vx(1:nx,:) = eye(nx);        % state-to-output matrix in lagrange term
Vu = zeros(ny,nu); Vu(nx+1:ny,:) = eye(nu);     % input-to-output matrix in lagrange term
Vx_e = zeros(ny_e,nx); Vx_e(1:nx,:) = eye(nx);  % state-to-output matrix in mayer term
W = diag([5*2, 0, 0, 0.5*2, 0.05*2]);
W_e = W(1:ny_e,1:ny_e);
y_ref = zeros(ny,1);                            % set intial references
y_ref_e = zeros(ny_e,1);

% constraint
constr_type = 'bgh';
dyn_type = 'explicit';
x0 = [0.1; 0; 0; 0];
Jbx = eye(nbx,nx);
lbx = [-0.2; -1; -1; -0.3];
ubx = [0.4; 1; 1; 0.5];
Jbu = eye(nbu,nu);
lbu = -0.3;
ubu = 0.5;

%% acados ocp model
ocp_model = acados_ocp_model();
% ocp_model.set('name', model_name);

% end time
ocp_model.set('T', T);

% symbolics
ocp_model.set('sym_x', model.sym_x);
ocp_model.set('sym_u', model.sym_u);
ocp_model.set('sym_xdot', model.sym_xdot);

% cost
ocp_model.set('cost_type', cost_type);
ocp_model.set('cost_type_e', cost_type_e);
ocp_model.set('cost_Vx', Vx);
ocp_model.set('cost_Vu', Vu);
ocp_model.set('cost_Vx_e', Vx_e);
ocp_model.set('cost_W', W);
ocp_model.set('cost_W_e', W_e);
ocp_model.set('cost_y_ref', y_ref);
ocp_model.set('cost_y_ref_e', y_ref_e);

% constraint
ocp_model.set('dyn_type', dyn_type);            
ocp_model.set('dyn_expr_f', model.expr_f_expl); 
ocp_model.set('constr_x0', x0);                 % dynamic
ocp_model.set('constr_type', constr_type);
ocp_model.set('constr_Jbx', Jbx);
ocp_model.set('constr_lbx', lbx);
ocp_model.set('constr_ubx', ubx);
ocp_model.set('constr_Jbu', Jbu);
ocp_model.set('constr_lbu', lbu);
ocp_model.set('constr_ubu', ubu);

disp('ocp_model.model_struct: ')
disp(ocp_model.model_struct)

%% acados ocp opts
ocp_opts = acados_ocp_opts();

% Code generation
ocp_opts.set('compile_interface', compile_interface);
ocp_opts.set('codgen_model', codgen_model);
ocp_opts.set('compile_model', compile_model);
ocp_opts.set('output_dir', output_dir);

% Shooting nodes
ocp_opts.set('param_scheme_N', param_scheme_N);

% Integrator
ocp_opts.set('sim_method', sim_method);
ocp_opts.set('sim_method_num_stages', sim_method_num_stages);
ocp_opts.set('sim_method_num_steps', sim_method_num_steps);
% ocp_opts.set('sim_method_newton_iter', sim_method_newton_iter);
ocp_opts.set('gnsf_detect_struct', gnsf_detect_struct);

% NLP solver
ocp_opts.set('nlp_solver', nlp_solver);
ocp_opts.set('qp_solver_iter_max', qp_solver_iter_max);
ocp_opts.set('nlp_solver_tol_stat', nlp_solver_tol_stat);
ocp_opts.set('nlp_solver_tol_eq', nlp_solver_tol_eq);
ocp_opts.set('nlp_solver_tol_ineq', nlp_solver_tol_ineq);
ocp_opts.set('nlp_solver_tol_comp', nlp_solver_tol_comp);
ocp_opts.set('nlp_solver_ext_qp_res', nlp_solver_ext_qp_res);
ocp_opts.set('nlp_solver_step_length', nlp_solver_step_length);
ocp_opts.set('rti_phase', rti_phase);

% QP solver
ocp_opts.set('qp_solver', qp_solver);
ocp_opts.set('qp_solver_iter_max', qp_solver_iter_max);
ocp_opts.set('qp_solver_cond_N', qp_solver_cond_N);
ocp_opts.set('qp_solver_cond_ric_alg', qp_solver_cond_ric_alg);
ocp_opts.set('qp_solver_ric_alg', qp_solver_ric_alg);
ocp_opts.set('qp_solver_warm_start', qp_solver_warm_start);
% ocp_opts.set('nlp_solver_warm_start_first_qp', warm_start_first_qp);

% Globalization
ocp_opts.set('globalization', globalization);
% ocp_opts.set('alpha_min', alpha_min);
% ocp_opts.set('alpha_reduction', alpha_reduction);

% Hessian approximation
ocp_opts.set('nlp_solver_exact_hessian', nlp_solver_exact_hessian);
ocp_opts.set('regularize_method', regularize_method);
ocp_opts.set('levenberg_marquardt', levenberg_marquardt);
% ocp_opts.set('exact_hess_dyn', exact_hess_dyn);
% ocp_opts.set('exact_hess_cost', exact_hess_cost);
% ocp_opts.set('exact_hess_constr', exact_hess_constr);

% Other
ocp_opts.set('print_level', print_level);

disp('ocp_opts.opts_struct: ');
disp(ocp_opts.opts_struct);

%% create ocp solver
ocp = acados_ocp(ocp_model, ocp_opts);

%% Simulation
Duration = 10;
N_sim = Duration/h;

% initialize data structs
x_sim = zeros(nx, N_sim+1);
u_sim = zeros(nu, N_sim+1);
cost_sim = zeros(1, N_sim+1);
x_sim(:, 1) = x0;
u_sim(:, 1) = zeros(nu, 1);
cost_sim(1, 1) = 0;

% set trajectory initialization (also can use plant: create acados integrator)
ocp.set('init_x', x0 * ones(1,param_scheme_N+1));
% ocp.set('init_x', zeros(nx,param_scheme_N+1));
ocp.set('init_u', zeros(nu, param_scheme_N));

% time-varying reference trajectory
x1ref_FUN = @(t) 0.4.*(-(0.5./(1+exp(t./0.1-0.8))) + (1./(1+exp(t./0.1-30))) - 0.4);
t = 0:h:Duration;
x1ref = 0.4.*(-(0.5./(1+exp(t./0.1-0.8))) + (1./(1+exp(t./0.1-30))) - 0.4);

% run mpc
fprintf('Simulation started.  It might take a while...\n')
tic;
for i = 1:N_sim
    
    % update reference
    t_ref = (i-1:i+param_scheme_N).*h;
    x1_ref = x1ref_FUN(t_ref);
    for j = 0:param_scheme_N-1
        y_ref(1) = x1_ref(j+1);
        ocp.set('cost_y_ref', y_ref, j);
    end
    y_ref_e(1) = x1_ref(param_scheme_N+1);
    ocp.set('cost_y_ref_e', y_ref_e, param_scheme_N);

    % solve ocp
    ocp.solve();
    status = ocp.get('status');      % 0 - success
    if status ~= 0
        error(sprintf('acados returned status %d in closed loop iteration %d. Exiting.', status, i));
    end

    % get solution t0
    x0 = ocp.get('x', 0);
    u0 = ocp.get('u', 0);
    x_sim(:, i+1) = x0;
    u_sim(:, i+1) = u0;
    cost_sim(1, i+1) = ocp.get_cost();

    % update initial state
    x0 = ocp.get('x', 1);
    ocp.set('constr_x0', x0);
    
end
tElapsed = toc
fprintf('Simulation finished!\n')

%% Plot
figure; hold on; grid on;
plot(t, x_sim, t, x1ref, '--');
legend('x1', 'x2', 'x3', 'u', 'x1Ref');

figure; hold on; grid on;
plot(t, u_sim);
legend('udot');

figure; hold on; grid on;
plot(t, cost_sim);
legend('the cost curve');

%% go embedded to generate templated C code
% ocp.generate_c_code;
6

So if you set param_scheme_N = 100;
W = diag([5*2, 0.1, 0, 0.5*2, 0.005*2]);
It does not oscillate much.
As I said the horizon should be long enough.

1 Like
7

After I tried your parameters, the tracking effect became better. It is really a problem with parameters such as weights. Thank you so much! :smiling_face_with_three_hearts:

Also, may I ask if there is any skill in parameter setting? Is it set by experience, or can some heuristic methods be used to quickly find a better parameter?