here is the code bellow:
####Implementation nmpc sur la profondeur pour voir sil ya retard de reception de mesures reelles 10/12/2024
-- coding: utf-8 --
“”"
Created on Tue Dec 10 09:36:12 2024
@author: rbenazouz
“”"
Implementation NMPC with fixed communication (que la profondeur)
import sys
sys.path.insert(0, ‘/mnt/c/Users/rbenazouz/acados/interfaces/acados_template’)
import time
import socket # Import socket for UDP communication
import casadi as ca
import numpy as np
import matplotlib.pyplot as plt
from acados_template import AcadosOcp
from acados_template import AcadosOcpSolver # Import the Acados OCP solver
Dynamics
Define the number of states and controls
n_states = 2 # [z, w]
n_controls = 1 # [tau_z]
State and control variables
state = ca.MX.sym(‘state’, n_states)
control = ca.MX.sym(‘control’, n_controls)
Dynamics parameters
z, w = state[0], state[1]
tau_z = control[0]
m = 46.0 # Vehicle mass
d_z = 22.0 # Linear damping coefficient
g = 9.81 # Gravity
F = 15 # Buoyancy force
B = m * g + F # Total buoyancy force
Coefficients de traînée
d_z1 = 22 # Coefficient linéaire de traînée (kg/s)
d_z2 = 800 # Coefficient quadratique de traînée (kg/m)
Simplified dynamics
z_dot = w
drag = d_z1 * z_dot + d_z2 * z_dot**2 # Traînée totale
w_dot = (tau_z - drag * w - F) / m
state_dot = ca.vertcat(z_dot, w_dot)
CasADi dynamics function
f_dynamics = ca.Function(‘f_dynamics’, [state, control], [state_dot])
Discretization of dynamics
dt = 0.05 ## a corrige
NMPC Configuration
ocp = AcadosOcp()
ocp.model.name = ‘depth_control’
ocp.model.x = state
ocp.model.u = control
ocp.model.f_expl_expr = state_dot
ocp.dims.N = 4 # Prediction horizon
ocp.solver_options.tf = ocp.dims.N * dt
Matrices de coût
#Q = np.diag([5000000000000000, 50]) # Poids pour [z, w] _ np.diag([5000000000, 0])
Q = np.diag([500000,500000 ]) # Poids pour [z, w] _ np.diag([5000000000, 0])
R = np.array([[0]]) # Poids pour tau_z np.array([[0.001]])
W = np.block([[Q, np.zeros((n_states, n_controls))],
[np.zeros((n_controls, n_states)), R]])
Terminal weight matrix
W_e = Q # Terminal weight matrix
Set cost weights in Acados OCP
ocp.cost.W = W
ocp.cost.W_e = W_e
Define selection matrices for cost function
Vx = np.eye(n_states) # Select all states
Vu = np.eye(n_controls) # Select all controls
Vx_e = np.eye(n_states) # Terminal state cost selection
Configurer les références
ocp.cost.cost_type = ‘LINEAR_LS’ # Type de coût (Least Squares)
ocp.cost.cost_type_e = ‘LINEAR_LS’ # Coût terminal
Update cost selection matrices
ocp.cost.Vx = np.vstack([Vx, np.zeros((n_controls, n_states))])
ocp.cost.Vu = np.vstack([np.zeros((n_states, n_controls)), Vu])
ocp.cost.Vx_e = Vx_e
ocp.cost.yref = np.zeros((n_states + n_controls,))
ocp.cost.yref_e = np.zeros((n_states,))
Constraints
ocp.constraints.lbu = np.array([-50.0]) # Lower bound for tau_z
ocp.constraints.ubu = np.array([50.0]) # Upper bound for tau_z
ocp.constraints.idxbu = np.arange(n_controls)
ocp.solver_options.nlp_solver_max_iter = 100
Initialize solver
ocp_solver = AcadosOcpSolver(ocp, json_file=‘acados_ocp.json’)
Warm up the NMPC solver
initial_state = np.zeros((n_states,)) # Initial state [z=0, w=0]
ocp_solver.set(0, ‘x’, initial_state) # Set the initial state in the solver
for k in range(ocp.dims.N): # For each prediction horizon step
ocp_solver.set(k, ‘yref’, np.zeros((n_states + n_controls,))) # Set dummy reference
ocp_solver.solve() # Run a warm-up solve to initialize solver’s internal states
t_end = 60
time_array = np.arange(0, t_end, dt)
ZINI, ZINTER, ZF, TF, T_STABLE = 0.0, 0.5, 0.25, 20.0, 10.0
def poly5_trajectory(t, t_start, t_end, z_start, z_end):
“”"
Generates a 5th-order polynomial trajectory.
:param t: Current time.
:param t_start: Start time.
:param t_end: End time.
:param z_start: Start position.
:param z_end: End position.
:return: Position z(t).
“”"
T = t_end - t_start
if t < t_start:
return z_start, 0.0 # z and its derivative w
elif t > t_end:
return z_end, 0.0 # z and its derivative w
else:
a0 = z_start
a1 = 0
a2 = 0
a3 = 10 * (z_end - z_start) / T3
a4 = -15 * (z_end - z_start) / T4
a5 = 6 * (z_end - z_start) / T5
tau = t - t_start
z_t = a0 + a1 * tau + a2 * tau2 + a3 * tau3 + a4 * tau4 + a5 * tau5
w_t = a1 + 2a2 * tau + 3a3 * tau2 + 4 * a4 * tau3 + 5 * a5 * tau4
return z_t, w_t
Generate reference trajectories
z_trajectory =
w_trajectory =
for t in time_array:
if t < TF:
# Transition from ZINI to ZINTER
z_t, w_t = poly5_trajectory(t, 0, TF, ZINI, ZINTER)
elif t < TF + T_STABLE:
# Steady state at ZINTER
z_t, w_t = ZINTER, 0.01 # Add a small non-zero zdot (w_t)
elif t < 2 * TF + T_STABLE:
# Transition from ZINTER to ZF
z_t, w_t = poly5_trajectory(t, TF + T_STABLE, 2 * TF + T_STABLE, ZINTER, ZF)
else:
# Steady state at ZF
z_t, w_t = ZF, 0.01 # Add a small non-zero zdot (w_t)
z_trajectory.append(z_t)
w_trajectory.append(w_t)
Generate reference trajectories
z_trajectory =
w_trajectory =
for t in time_array:
if t < TF:
z_t, w_t = poly5_trajectory(t, 0, TF, ZINI, ZINTER)
elif t < TF + T_STABLE:
z_t, w_t = ZINTER, 0.0
elif t < 2 * TF + T_STABLE:
z_t, w_t = poly5_trajectory(t, TF + T_STABLE, 2 * TF + T_STABLE, ZINTER, ZF)
else:
z_t, w_t = ZF, 0.0
z_trajectory.append(z_t)
w_trajectory.append(w_t)
The resulting z_trajectory contains the depth reference, and w_trajectory contains the rate of change (velocity) reference.
Start the control loop
start_time = time.time()
Control Loop
Update global index based on elapsed time
Calculate current_time and global_idx
current_time = time.time() - start_time # Elapsed time since the script started
global_idx = int(current_time / dt) # Update global index based on elapsed time
actual_trajectory =
actual_w_trajectory =
control_inputs =
errors =
Initialize storage for plots
control_inputs = # To store control input values
trajectory_errors = # To store trajectory errors
cost_function_values = # To store the cost function values
yref_segments_over_time = # Initialize a list to store yref_segment values
Initialization Phase
print(“Starting initialization phase…”)
Warm up the NMPC solver
initial_state = np.array([z_trajectory[0], 0.0]) # Match initial depth
Debug: Check the initial state
print(f"Expected initial state: [z = {z_trajectory[0]}, w = 0.0]“)
print(f"Setting initial state in solver: {initial_state}”)
Set the initial state in the solver
ocp_solver.set(0, ‘x’, initial_state)
Debug: Log warm-up references for all prediction horizon steps
for k in range(ocp.dims.N):
yref_debug = np.zeros((n_states + n_controls,))
print(f"Warm-up reference yref at k={k}: {yref_debug}")
ocp_solver.set(k, ‘yref’, yref_debug) # Set dummy reference
Run solver warm-up
print(“Running solver warm-up…”)
status = ocp_solver.solve() # Run a warm-up solve to initialize solver’s internal states
Debug: Check solver status
if status != 0:
print(f"Solver warm-up failed with status {status}. Exiting…")
sys.exit(1)
else:
print(“Solver warm-up completed successfully.”)
print(“Initialization phase complete.”)
Start the control loop
Address and ports for communication
DEST_IP = “192.168.0.17”
DEST_PORT = 5816
Create a UDP socket for receiving robot states
recv_socket = socket.socket(socket.AF_INET, socket.SOCK_DGRAM)
recv_socket.bind((“”, 5825))
print(“Waiting for UDP frames on port 5825…”)
Create a socket for sending control commands
send_socket = socket.socket(socket.AF_INET, socket.SOCK_DGRAM)
recv_socket.settimeout(0.1) # Avoid hanging
Begin Control Loop
Begin Control Loop
while True:
try:
current_time = time.time() - start_time # Elapsed time since control loop started
# Receive current state
try:
recv_time = time.time() # Moment où l'état est reçu
data, address = recv_socket.recvfrom(1024)
#print(f"[{recv_time:.3f}s] Received state: {data.decode('utf-8')}")
except socket.timeout:
print(f"[{time.time():.3f}s] No state received (timeout). Skipping...")
continue # Skip iteration if no data received
fields = data.decode('utf-8').strip().split(',')
if len(fields) < 22 or fields[0] != 'I' or fields[13].strip() != 'J':
print(f"[{current_time:.2f}s] Malformed frame skipped.")
continue
# Extract values
ROV_z = float(fields[3])
ROV_w = float(fields[9]) / 100
#print(f"[{ROV_w:.2f}s] ")
# Set initial state for solver
initial_state = np.array([ROV_z, ROV_w])
ocp_solver.set(0, 'x', initial_state)
yref_segment_list = [] # Temporary list to store segments for current time step
# Update reference trajectory
for k in range(ocp.dims.N):
ref_idx = min(global_idx + k, len(z_trajectory) - 1)
yref_segment = np.array([z_trajectory[ref_idx],w_trajectory[ref_idx], 0.0])
ocp_solver.set(k, 'yref', yref_segment)
yref_segment_list.append(yref_segment[0]) # Save the depth reference
# Debugging: Print global_idx, ref_idx, and the corresponding value in z_trajectory
#print(f"global_idx: {global_idx}, ref_idx at k={k}: {ref_idx}, z_trajectory[ref_idx]: {z_trajectory[ref_idx]}")
#print(f"At global_idx={global_idx}, ref_idx={ref_idx}, yref_segment={yref_segment}")
print(f"t={current_time:.2f}, z_ref={z_trajectory[global_idx]:.2f}, zdot_ref={w_trajectory[global_idx]:.2f}")
yref_segments_over_time.append(yref_segment_list) # Store all segments for the time step
# Terminal reference
terminal_idx = min(global_idx + ocp.dims.N, len(z_trajectory) - 1)
yref_terminal = np.array([z_trajectory[terminal_idx], 0.0])
ocp_solver.set(ocp.dims.N, 'yref', yref_terminal)
# Solve OCP
status = ocp_solver.solve()
print(f"Solver status at t={current_time:.2f}: {status}")
if status != 0:
print(f"Solver failed with status {status}")
tau_z_optimal = 0.0 # Default to a safe value if solver fails
else:
# Extract optimal control input
tau_z_optimal = ocp_solver.get(0, 'u')[0]
# **Add Data Collection Here**
# Store control input
control_inputs.append(tau_z_optimal)
# Compute and store trajectory error
error = z_trajectory[global_idx] - ROV_z
trajectory_errors.append(error)
# Retrieve and store cost function value
cost_value = ocp_solver.get_cost()
cost_function_values.append(cost_value)
# Store actual trajectory for analysis
actual_trajectory.append(ROV_z)
# Store actual zdot (w)
actual_w_trajectory.append(ROV_w)
# Send control command
send_time = time.time() # Moment où la commande est envoyée
response_message = f"S,0.00,0.00,{tau_z_optimal:.2f},0.000,0.000,0.000$\n"
send_socket.sendto(response_message.encode('utf-8'), (DEST_IP, DEST_PORT))
#print(f"[{send_time:.3f}s] Sent control command: {response_message.strip()}")
# Update global index
global_idx += 1
if global_idx >= len(z_trajectory):
print("Trajectory complete. Stopping control loop.")
break
except Exception as e:
print(f"Error: {e}")
break
Plot results
plt.figure()
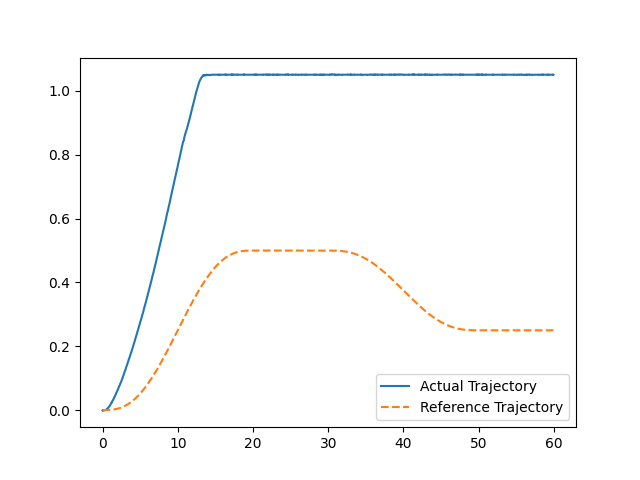
plt.plot(time_array[:len(actual_trajectory)], actual_trajectory, label=“Actual Trajectory”)
plt.plot(time_array, z_trajectory, label=“Reference Trajectory”, linestyle=“–”)
plt.legend()
plt.savefig(‘trajectory_vs_reference_depth_35.png’)
plt.show()
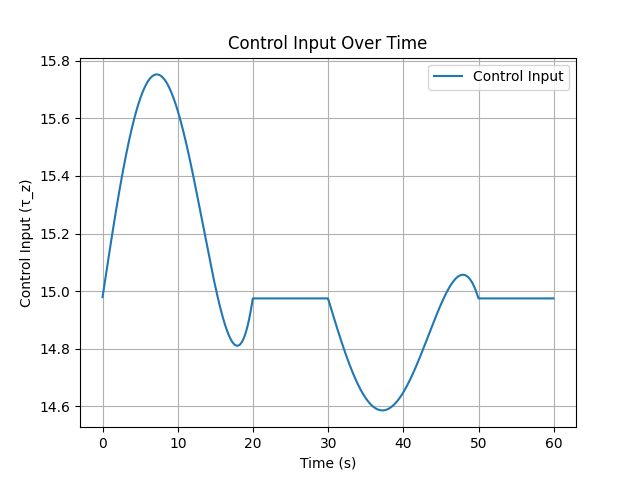
plt.figure()
plt.plot(time_array[:len(control_inputs)], control_inputs, label=“Control Input”)
plt.xlabel(“Time (s)”)
plt.ylabel(“Control Input (τ_z)”)
plt.title(“Control Input Over Time”)
plt.legend()
plt.grid()
plt.savefig(‘Control_input_depth_35.png’)
plt.show()
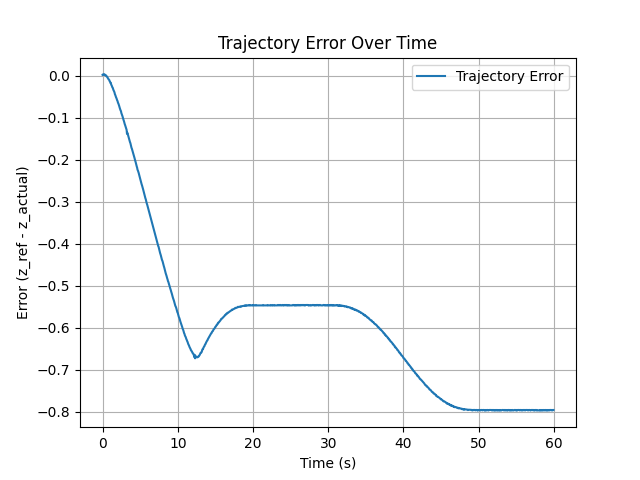
plt.figure()
plt.plot(time_array[:len(trajectory_errors)], trajectory_errors, label=“Trajectory Error”)
plt.xlabel(“Time (s)”)
plt.ylabel(“Error (z_ref - z_actual)”)
plt.title(“Trajectory Error Over Time”)
plt.legend()
plt.grid()
plt.savefig(‘Trajectory_error_depth_35.png’)
plt.show()
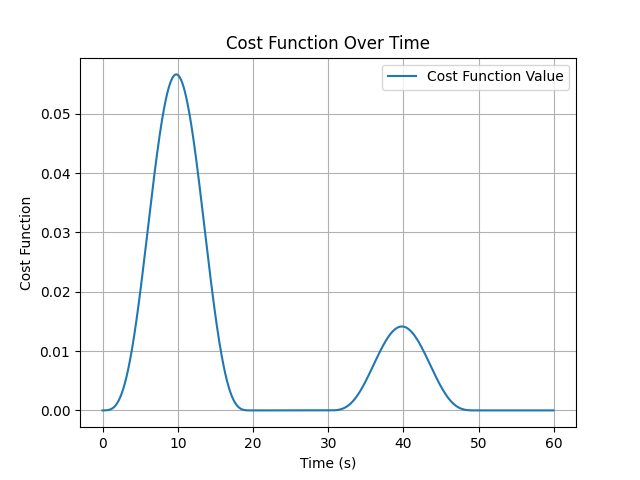
plt.figure()
plt.plot(time_array[:len(cost_function_values)], cost_function_values, label=“Cost Function Value”)
plt.xlabel(“Time (s)”)
plt.ylabel(“Cost Function”)
plt.title(“Cost Function Over Time”)
plt.legend()
plt.grid()
plt.savefig(‘Cost_Function_depth_35.png’)
plt.show()
plt.figure()
plt.plot(time_array[:len(actual_w_trajectory)], actual_w_trajectory, label=“Actual zdot (w)”)
plt.plot(time_array, w_trajectory, label=“Reference zdot (w_ref)”, linestyle=“–”)
plt.xlabel(“Time (s)”)
plt.ylabel(“zdot (w)”)
plt.title(“zdot (w) Actual vs Reference”)
plt.legend()
plt.grid()
plt.savefig(‘zdot_actual_vs_reference_depth_35.png’) # Save the plot
plt.show()
Convert list of lists to numpy array for easier indexing
yref_segments_over_time = np.array(yref_segments_over_time)
Plot the reference trajectory segments over time
time_steps = np.arange(len(yref_segments_over_time)) * dt # Generate time array
plt.figure(figsize=(10, 6))
for k in range(ocp.dims.N):
plt.plot(time_steps, [segment[k] for segment in yref_segments_over_time], label=f"Prediction Horizon Step {k + 1}")
plt.xlabel(“Time (s)”)
plt.ylabel(“Reference Trajectory (z)”)
plt.title(“Reference Trajectory Segments Over Time”)
plt.legend()
plt.grid()
plt.savefig(“yref_segments_plot_34.png”) # Save the plot
plt.show()