External Cost Function with Integral

User Questions
1

Hi :waving_hand:

I am trying to implement an NMPC simulation in acados.
My cost function differs slightly from the conventional one, so I would like to use the "EXTERNAL" cost type; however, I am unsure how to implement it.

The NMPC cost I want to realize is as follows (ref: https://onlinelibrary.wiley.com/doi/10.1002/rnc.70083):

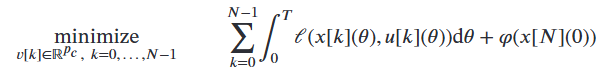
ocp_function

where \ell(x,u) and \varphi(x) denote the stage cost and terminal cost, respectively, both defined in quadratic form.

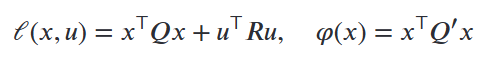
cost_function

In particular, the stage cost contains an integral over the sampling period.
Assuming a zero-order hold (ZOH) on the control input during each interval, I would like to approximate this integral more accurately using Simpson’s rule. This requires subdividing the sampling interval into smaller segments and applying the Simpson approximation, which typically involves a for-loop style computation.

From what I have seen, most example codes do not use such integral-type costs.
Could you give me some advice on how to implement this kind of integral cost in acados? Also, if there are more common or recommended ways to handle such integral costs, I would be very interested to learn about them.

I really appreciate any help you can provide.

2

Hi,

the acados interface actually takes the path cost function in continuous time and then “integrates” them over the shooting intervals.
However, by default, this integration is basically an explicit Euler scheme.
A more precise one is implemented for IRK and Nonlinear least-squares or convex-over-nonlinear cost terms.
This is described and compared to the default, the “shooting node cost discretization” in our paper:
Gauss–Newton Runge–Kutta integration for efficient discretization of optimal control problems with long horizons and least-squares costs.

A more precise integration of the cost term with for-loops and the simpson rule, is likely less efficient as it would require to basically integrate your system additionally in the cost module using casadi expressions.

Best,
Jonathan