Bipedal robot footstep planner

User Questions
1

Hi Acados community,

I’m currently using the python acados interface and we are trying to write an MPC which regulates the zero moment point of a LIP. We use this as an approximation for our bipedal walker. From the MPC, we need to extract amongst others, the footstep positions and the CoM trajectory.

To impose certain constraints we also need the previous footsteps. Every time a new footstep is set, the old footstep positions have to be switched. One of the problems is that the footstep switch timing is not in line with with the MPC timing. Namely, the footsteps only have to be switched every 4 shooting nodes, not every single shooting node.

From what I have seen from other forum posts, the best way to tackle this is to put both the current footsteps and the previous footsteps in the state vector. The derivative of the previous footstep would be x_pos (current footstep) - x_pos_prev (prevous footstep). By passing a model parameter called “switch”, we make sure the derivative of the previous footstep is only calculated at the moment when a new footstep is set. The “switch” parameter is 1 for every 4 shooting nodes, and 0 for everything in between.

    eta = np.sqrt(g/h_c)
    f_expl = vertcat(dxcom,
                     (eta**2)*xcom-(eta**2)*xzmp,
                     dxzmp,
                     dycom,
                     (eta**2)*ycom-(eta**2)*yzmp,
                     dyzmp,
                     newstep_xdot,
                     -switch*xpos_prev+switch*xpos,
                     newstep_ydot,
                     -switch*ypos_prev-switch*ypos)

With newstep_xdot and newstep_ydot being the rate of change for the new footstep.

We hardcoded when i = 0 because the bipedal walker at that moment is in double stance, which has different dynamics from when it is in single stance. The periodic walking after taking of should correspond to:

    elif i != 0 and i%(N/len(plan_footsteps[0]))==0:
        index+=1
        count = -count

        ocp_solver.set(i, "p", np.array([plan_footsteps_delta[0], -count*plan_footsteps_delta[1], 1]))

With index going up our footstep reference planning and count switching the axis for the y positions, which need to be either +0.1 or -0.1.

Now that the problem formulation is described, our problem is that when we want to update the x_pos_prev and y_pos_prev, the values are not what we expect. x_pos and y_pos work perfectly but the x_pos_prev and y_pos_prev values don’t correspond to the previous footsteps. Does this have something to do with the integrator that is used?

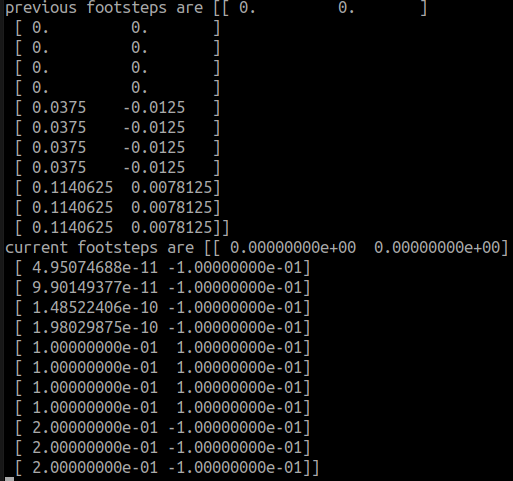
image

The image shows the printed previous and current footsteps.

Can you please help us on what might be going wrong?

Thank you in advance!

Kind greetings,
Jack

2

Update: we solved the problem by switching the amount of integrator stages from 4 to 1. In our understanding (correct me if I’m wrong), by doing this we use a standard forward Euler integration instead of an RK4, which messes up our (every-shooting-node) footstep variable integration.

3

Hi Jack,

maybe I am missing something, but why can’t you make those previous footsteps parameters and update them whenever a new step has been made?

Anyway, great you solved your issue for now.

Cheers!

4

Hey @FreyJo ,

The final footsteps are decided by solving the cost function, which are based on desired footstep positions that we pass as parameters. So in our understanding, there was no way to get the previous solution (x_pos[k-1]) from the solver and pass it as a parameter to the x_pos_prev variable. Is this due to the fact that the solver makes use of multiple shooting?

Kind regards,
Jack

5

Hey @FreyJo ,

The initial problem of getting the previous footsteps that happens every 6 (depending on N) shooting node steps now work by switching to forward euler integration instead of RK4. However, because part of the problem is depended on every shooting node step (let’s call this part A) and part of it is only depended on every 6 shooting node steps (let’s call this part B), we run into difficulties with part A.

Part A displays a centre of mass trajectory of our bipedal robot that takes the form on approximately a sine function. With forward euler, this trajectory diverges eventually. We feel like we should use RK4 integration for part A, but this messes up the integration happening in part B.

Do you have a suggestion on how we can solve this problem?
reminder: the previous footsteps that we need to take, are just the previous solutions from one of our state variables. If there is a way to be able to take these solutions and feed them as parameters while solving, that would solve the problem I think.

6

You can just set the parameters to the values corresponding to the old solution in between the solver calls.
It would not really make sense to update parameters “while” solving the problem IMO.