Hi ![]()
I’m using the acados python interface for a robot footstep planner and as of now, I’m facing this problem where the decision variable “footstep_length_x” gets smaller when the timestep dt = Tf/N gets too small at some point. The decision variable is decided by the cost function where we pass a reference footstep length as a parameter with a really big weight factor. For now, this reference parameter is always 0.2 meters. When dt is large enough the decision variable footstep_length_x will be set to 0.2 meters but when the time horizon and thus the dt gets smaller, the decision variable footstep_length_x for some reason also becomes smaller.
The footstep part of the cost function has the form of:
beta*(model.u[2]-model.p[0])**2+(model.u[3]-model.p[1])**2)
Where beta is the big weight factor for determining the footstep sizes in x and y. (which for x is set to 0.2, for y it is set to 0.1).
The current solution with Tf = 13 and N = 60 looks like:
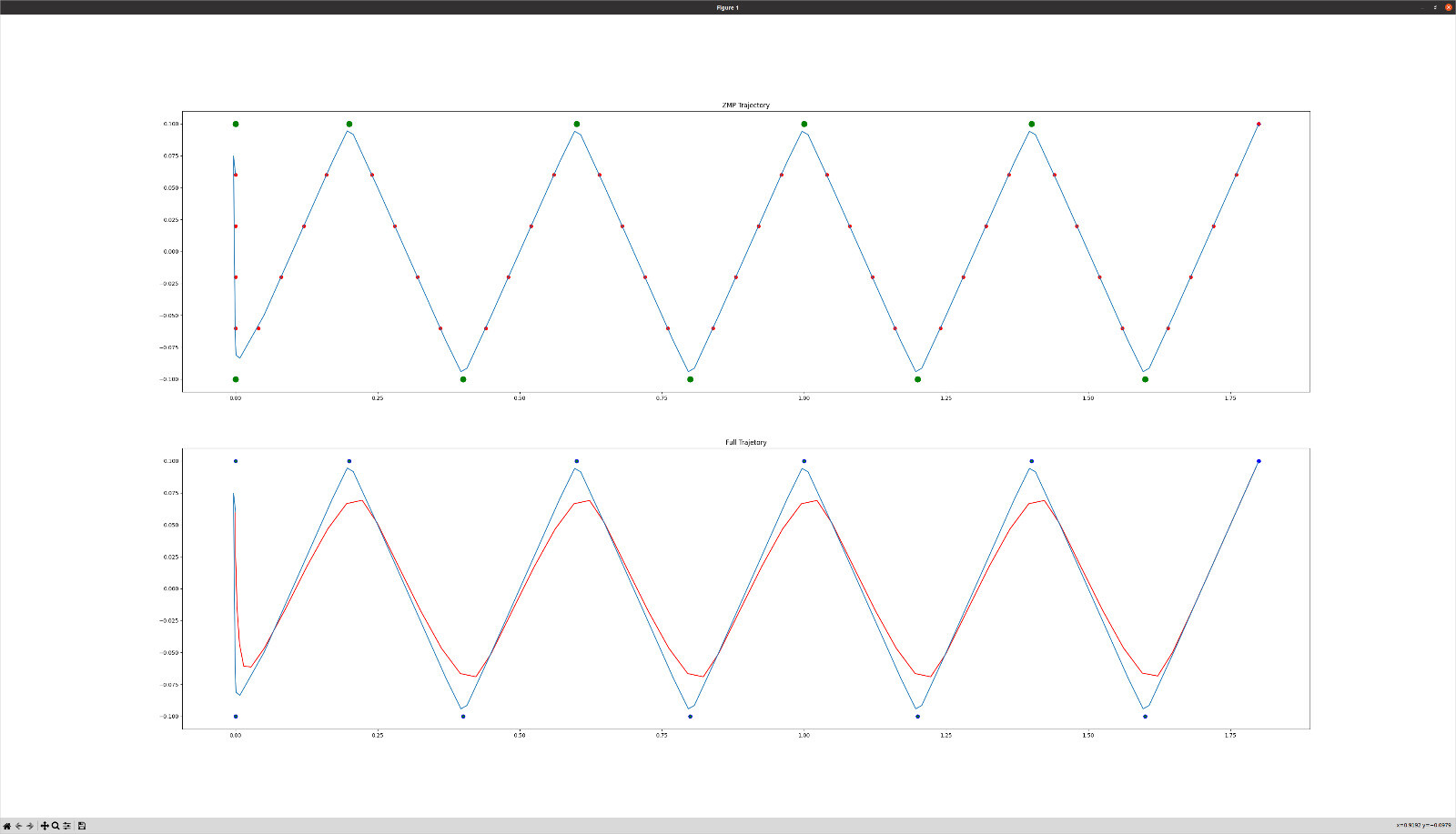
Where the dots in both plots represent the footsteps. The red line represents to CoM of the robot and the blue line represents the zero moment point. It can be seen that in this solution, the footstep_length_x is always 0.2 (except for the first step).
But when the time horizon is set to Tf = 7 and N stays at N = 60, the solution looks like:
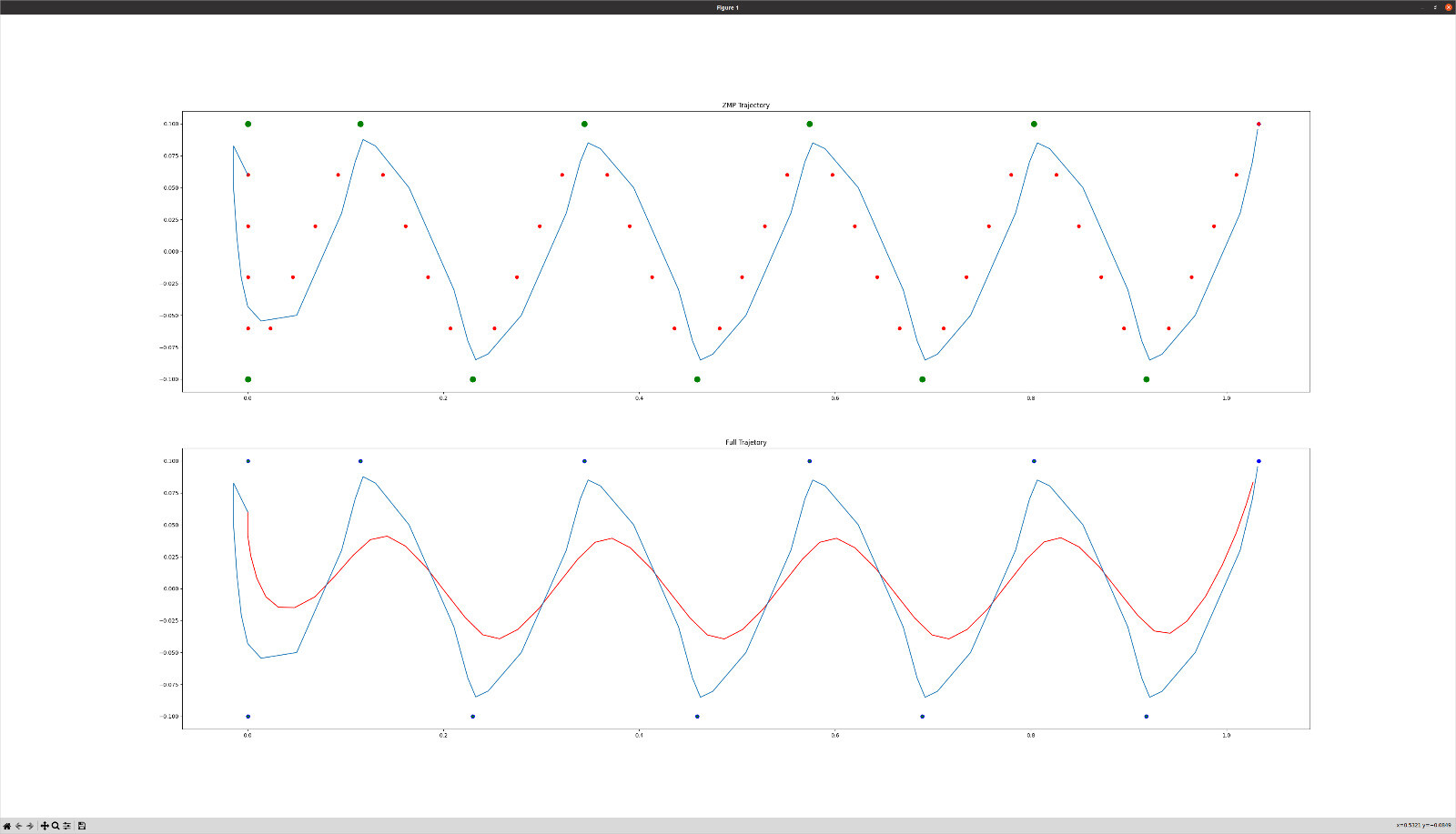
Here it can be seen that the footstep_length_x becomes smaller than 0.2 (about 0.11).
This also happens when all the applied constraints are removed and the cost function is simplified to only the footstep planning (without the CoM and ZMP).
How can the dt affect the solution that much? especially the footstep_length_x? and how come the footstep_length_y doesn’t change?
Thanks in advance!
Kind regards,
Jack