Hi everyone,
I’m developing a project that uses acados NMPC solver to optimally control a racing vehicle. So far, everything is being done in a simulation. I’m trying things out and I noticed a weird behaviour. I will describe my environment setup and then I will expose the problem.
The objective is to make my simulated vehicle follow a closed-loop racing line in real time. I used the acados Python interface to generate the C code, and then I created a ROS 2 node in C++ to integrate this controller with the simulator.
The simulator takes in input a control command (target speed and target steering angle) and continuously outputs the current state (x, y, speed and yaw) of the vehicle in a 2D map. The yaw is always outputted in the range [-pi, pi). The NMPC controller just sends the control command, it does not interact in any other way with the sim.
The car model is defined by:
where L is the wheelbase of the car, K_v is the proportional gain of the speed, u_1 is the target speed and u_2 is the target steering angle.
The racing line is used as the reference trajectory for the NMPC. The attributes of the racing line that I’m using are the x and y coordinates of the waypoints on the map, the yaw angle at each waypoint (between [-pi, pi)) and the target speed at each waypoint.
Each waypoint is separated by a distance of 0.05 meters.
Important note: since we fix an horizon N and a time prediction horizon tf, and we know at every iteration the total length of the reference trajectory (N * 0.05), the solution trajectory is constrained to have a mean velocity of 0.05 * N / tf m/s. This is important because the solver is not totally free to choose the velocity of the vehicle, and therefore the speed reference is not considered in the cost function.
The problem
The C++ code compiles and works. By visualizing the solution trajectory on the sim, I can see that the vehicle is following the racing line very well.
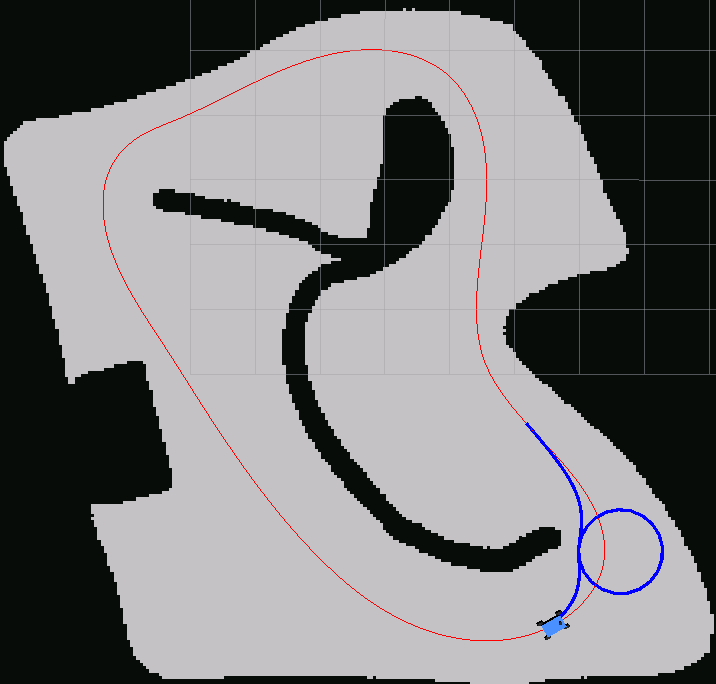
However, in a specific point of a map, the solution trajectory (in blue in the image) creates these weird circles before returning to the racing line. The circles are not present in the reference trajectory (in red in the image).
This happens deterministically on every combination of map and racing line that I tried. Once the circle is created, it goes forward also after the critical point (1), even in places where it was not there before. It’s as if it reaches a “local minimum” of the solution and it gets stuck there (even though when changing mode from SQP_RTI to SQP, the solver returns status code 2, i.e., max iter reached, which are 100 in this case).
Another important note: in the current model definition, theta is not constrained to be in the range [-pi, pi), neither in the model nor in the solution trajectory.
Then it makes sense! The car is rotating, and so the theta of the solution increases and it would get out of the said range (2). So the solver tries to minimize the cost by rotating the car in the opposite direction, creating the circle and therefore coming back to the correct theta range.
But:
- the first weird behaviour is that when the car returns close to the critical point after completing a lap, another circle is created. After three laps, three circles are created. This does not make sense to me. These circles, again, remain and are moved forward also after the critical point.
- this happens also when the cost on
thetais not considered. I tried to set the cost onthetato zero, code regenerated and recompiled, but the circles are still there. Why is this happening? - another weird thing I noticed is that sometimes, just before the circle creation, the solver outputs a nonsense solution, like a straight line that goes out of the map. I cannot see that all the time, but one reason could be that the solver terminates in around 1 ms, so it is difficult to detect it.
- when lowering the upper bound of the target speed to
(0.05 * N / tf) + 0.1m/s, the problem disappears. It makes sense, because doing the circle means indirectly increasing the speed (since more distance is covered in the same time and the mean speed is constrained). Of course, this is not how I want to solve the problem.
The racing line (the reference) has been checked thoroughly and it is correct. To be more precise, the critical point is where (2) holds, and as written above the reference theta is always between [-pi, pi). By the way, this problem happens also when the reference is unconstrained. In my opinion, the problem is in the way I’m using the solver.
In the provided C++ code, is there a problem with the initial solution or a conflict between how acados stores internally the solution and my code? Does the solver automatically do a warm start? It seems so, because of (1).
If you need more information, tell me. Thank you in advance.
Model
def export_ode_kin_car_model():
model_name = 'kin_car'
# parameters
L = 0.321 # wheelbase
K_v = 10.0 # velocity gain
# States (f_exp)
x = SX.sym('x')
y = SX.sym('y')
theta = SX.sym('theta')
v = SX.sym('v')
x = vertcat(x, y, theta, v)
# Controls
u_1 = SX.sym('u_1') # velocity
u_2 = SX.sym('u_2') # steering angle
u = vertcat(u_1, u_2)
# For f_impl
x_dot = SX.sym('x_dot')
y_dot = SX.sym('y_dot')
theta_dot = SX.sym('theta_dot')
v_dot = SX.sym('v_dot')
xdot = vertcat(x_dot, y_dot, theta_dot, v_dot)
# Model equations
dx = v * ca.cos(theta)
dy = v * ca.sin(theta)
dtheta = (v / L) * ca.tan(u_2)
dv = K_v * (u_1 - v)
# Explicit and implicit functions
f_expl = vertcat(dx, dy, dtheta, dv)
f_impl = xdot - f_expl
# algebraic variables
z = []
# parameters
p = []
# dynamics
model = AcadosModel()
model.f_impl_expr = f_impl
model.x = x
model.xdot = xdot
model.u = u
model.z = z
model.p = p
model.name = model_name
return model
C code generation
ocp = AcadosOcp()
# export model
model = export_ode_kin_car_model()
ocp.model = model
N = 80
Tf = 2.0
nx = model.x.rows()
nu = model.u.rows()
# set prediction horizon
ocp.solver_options.N_horizon = N
ocp.solver_options.tf = Tf
Q = np.eye(nx)
Q[0, 0] = 10.0 # x
Q[1, 1] = 10.0 # y
Q[2, 2] = 0.0 # theta
Q[3, 3] = 0.0 # v
R = np.eye(nu)
R[0, 0] = 0.1 # u_1
R[1, 1] = 1.0 # u_2
# path cost
ocp.cost.cost_type = 'NONLINEAR_LS'
ocp.model.cost_y_expr = ca.vertcat(model.x, model.u)
ocp.cost.yref = np.zeros((nx+nu,))
ocp.cost.W = ca.diagcat(Q, R).full()
# terminal cost
ocp.cost.cost_type_e = 'NONLINEAR_LS'
ocp.model.cost_y_expr_e = model.x
ocp.cost.yref_e = np.zeros((nx,))
ocp.cost.W_e = 10 * Q
# set constraints
ocp.constraints.lbu = np.array([0.5, -0.46])
ocp.constraints.ubu = np.array([8.0, 0.46])
ocp.constraints.idxbu = np.array([0, 1])
# To add x0 during model definition, otherwise it is not easily possible to set the initial state at runtime
ocp.constraints.x0 = np.array([0.0, 0.0, 0.0, 0.0])
## set QP solver
ocp.solver_options.qp_solver = 'PARTIAL_CONDENSING_HPIPM'
ocp.solver_options.integrator_type = 'IRK'
ocp.solver_options.nlp_solver_type = 'SQP'
acados_solver = AcadosOcpSolver(ocp, json_file='acados_ocp_kin_car.json')
ROS 2 node (C++ code)
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include "rclcpp/rclcpp.hpp"
#include "rclcpp/logging.hpp"
#include "acados/utils/print.h"
#include "acados/utils/math.h"
#include "acados_c/ocp_nlp_interface.h"
#include "acados_c/external_function_interface.h"
#include "acados_solver_kin_car.h"
// blasfeo
#include "blasfeo_d_aux_ext_dep.h"
#include <tf2/utils.h>
#include <nav_msgs/msg/odometry.hpp>
#include <geometry_msgs/msg/point.hpp>
#include <visualization_msgs/msg/marker.hpp>
#include <ackermann_msgs/msg/ackermann_drive_stamped.hpp>
#include "raceline_utils.hpp"
#define NX KIN_CAR_NX
#define NP KIN_CAR_NP
#define NU KIN_CAR_NU
#define NBX0 KIN_CAR_NBX0
#define NP_GLOBAL KIN_CAR_NP_GLOBAL
class NMPCNode : public rclcpp::Node {
public:
NMPCNode() : Node("nmpc_node") {
raceline_path_ = declare_parameter("raceline_path", "");
odom_topic_ = declare_parameter("odom_topic", "");
drive_topic_ = declare_parameter("drive_topic", "");
if (raceline_path_.empty()) {
RCLCPP_ERROR(get_logger(), "Raceline path is empty!");
exit(1);
}
if (odom_topic_.empty()) {
RCLCPP_ERROR(get_logger(), "Odometry topic is empty!");
exit(1);
}
if (drive_topic_.empty()) {
RCLCPP_ERROR(get_logger(), "Drive topic is empty!");
exit(1);
}
raceline.initialize(raceline_path_);
odom_subscriber_ = this->create_subscription<nav_msgs::msg::Odometry>(
odom_topic_, 1, std::bind(&NMPCNode::odom_callback, this, std::placeholders::_1));
drive_publisher_ = this->create_publisher<ackermann_msgs::msg::AckermannDriveStamped>(drive_topic_, 1);
marker_publisher_ = this->create_publisher<visualization_msgs::msg::Marker>("nmpc_path", 1);
// --- NMPC initialization ---
acados_ocp_capsule = kin_car_acados_create_capsule();
// There is an opportunity to change the number of shooting intervals in C without new code generation.
// Look at the associated header file for further information.
N = KIN_CAR_N;
// Allocate the array and fill it accordingly
double* new_time_steps = NULL;
status = kin_car_acados_create_with_discretization(acados_ocp_capsule, N, new_time_steps);
if (status) {
RCLCPP_ERROR(get_logger(), "kin_car_acados_create_with_discretization() returned status %d. Exiting.\n",
status);
exit(1);
}
nlp_config = kin_car_acados_get_nlp_config(acados_ocp_capsule);
nlp_dims = kin_car_acados_get_nlp_dims(acados_ocp_capsule);
nlp_in = kin_car_acados_get_nlp_in(acados_ocp_capsule);
nlp_out = kin_car_acados_get_nlp_out(acados_ocp_capsule);
nlp_solver = kin_car_acados_get_nlp_solver(acados_ocp_capsule);
nlp_opts = kin_car_acados_get_nlp_opts(acados_ocp_capsule);
x = (double*) malloc(KIN_CAR_NX * (KIN_CAR_N + 1) * sizeof(double));
u = (double*) malloc(KIN_CAR_NU * KIN_CAR_N * sizeof(double));
yref = (double*) malloc(KIN_CAR_NY * KIN_CAR_N * sizeof(double));
yref_e = (double*) malloc(KIN_CAR_NYN * sizeof(double));
RCLCPP_INFO(get_logger(), "NMPCNode initialized");
}
~NMPCNode() {
free(x);
free(u);
free(yref);
free(yref_e);
status = kin_car_acados_free(acados_ocp_capsule);
if (status) {
RCLCPP_ERROR(get_logger(), "kin_car_acados_free() returned status %d.", status);
}
status = kin_car_acados_free_capsule(acados_ocp_capsule);
if (status) {
RCLCPP_ERROR(get_logger(), "kin_car_acados_free_capsule() returned status %d.", status);
}
}
private:
std::string raceline_path_;
std::string odom_topic_;
std::string drive_topic_;
rclcpp::Subscription<nav_msgs::msg::Odometry>::SharedPtr odom_subscriber_;
rclcpp::Publisher<ackermann_msgs::msg::AckermannDriveStamped>::SharedPtr drive_publisher_;
rclcpp::Publisher<visualization_msgs::msg::Marker>::SharedPtr marker_publisher_;
int status;
kin_car_solver_capsule* acados_ocp_capsule;
ocp_nlp_config* nlp_config;
ocp_nlp_dims* nlp_dims;
ocp_nlp_in* nlp_in;
ocp_nlp_out* nlp_out;
ocp_nlp_solver* nlp_solver;
void* nlp_opts;
int N;
double* x;
double* u;
double* yref;
double* yref_e;
double xtraj[KIN_CAR_NX * (KIN_CAR_N + 1)];
double utraj[KIN_CAR_NU * KIN_CAR_N];
double cost_data;
int initial_nearest_index;
Raceline raceline;
bool first_solve_iteration = true;
void update_yref(const int& nearest_index) {
// Since `i` starts at 0, we are getting also `yref_0`
for (int i = 0; i < N; i++) {
RacelineRow row = raceline.get_raceline_row((nearest_index + i ) % raceline.get_num_points());
yref[i * KIN_CAR_NY + 0] = row.x_r;
yref[i * KIN_CAR_NY + 1] = row.y_r;
yref[i * KIN_CAR_NY + 2] = row.heading;
yref[i * KIN_CAR_NY + 3] = row.vx_mps;
yref[i * KIN_CAR_NY + 4] = 0.0f;
yref[i * KIN_CAR_NY + 5] = 0.0f;
}
RacelineRow row = raceline.get_raceline_row((nearest_index + N) % raceline.get_num_points());
yref_e[0] = row.x_r;
yref_e[1] = row.y_r;
yref_e[2] = row.heading;
yref_e[3] = row.vx_mps;
}
void odom_callback(const nav_msgs::msg::Odometry::SharedPtr msg) {
float x_current = msg->pose.pose.position.x;
float y_current = msg->pose.pose.position.y;
float yaw_current = tf2::getYaw(msg->pose.pose.orientation);
float speed_current = msg->twist.twist.linear.x;
RCLCPP_WARN(get_logger(), "x: %.3f, y: %.3f, yaw: %.3f, speed: %.3f", x_current, y_current, yaw_current, speed_current);
// Set x0
double lbx0[4] = {x_current, y_current, yaw_current, speed_current};
double ubx0[4] = {x_current, y_current, yaw_current, speed_current};
ocp_nlp_constraints_model_set(nlp_config, nlp_dims, nlp_in, 0, "lbx", lbx0);
ocp_nlp_constraints_model_set(nlp_config, nlp_dims, nlp_in, 0, "ubx", ubx0);
// Get the closest point on the raceline
int nearest_index = raceline.search_nearest_index(x_current, y_current);
update_yref(nearest_index);
RCLCPP_INFO(get_logger(), "nearest_index: %d", nearest_index);
// Set y_ref
for (int i = 0; i < N; i++) {
ocp_nlp_cost_model_set(nlp_config, nlp_dims, nlp_in, i, "yref", yref + i * KIN_CAR_NY);
}
ocp_nlp_cost_model_set(nlp_config, nlp_dims, nlp_in, N, "yref", yref_e);
// Solve the optimization problem
double min_time = 1e12;
double kkt_norm_inf;
double elapsed_time;
int sqp_iter;
status = kin_car_acados_solve(acados_ocp_capsule);
ocp_nlp_get(nlp_solver, "time_tot", &elapsed_time);
min_time = MIN(elapsed_time, min_time);
first_solve_iteration = false;
// Check if the solution is feasible
if (status == ACADOS_SUCCESS) {
// RCLCPP_INFO(get_logger(), "kin_car_acados_solve(): SUCCESS!");
} else {
RCLCPP_ERROR(get_logger(), "kin_car_acados_solve() failed with status %d.", status);
}
// Statistics
ocp_nlp_out_get(nlp_config, nlp_dims, nlp_out, 0, "kkt_norm_inf", &kkt_norm_inf);
ocp_nlp_get(nlp_solver, "sqp_iter", &sqp_iter);
RCLCPP_INFO(get_logger(), " SQP iterations %2d\n Elapsed time: %f [ms]\n KKT: %e",
sqp_iter, min_time*1000, kkt_norm_inf);
ocp_nlp_out_get(nlp_config, nlp_dims, nlp_out, 0, "u", u);
RCLCPP_WARN(get_logger(), "u_1 (velocity): %f, u_2 (steering angle): %f", u[0], u[1]);
// print solution and statistics
for (int ii = 0; ii <= nlp_dims->N; ii++)
ocp_nlp_out_get(nlp_config, nlp_dims, nlp_out, ii, "x", &xtraj[ii*NX]);
for (int ii = 0; ii < nlp_dims->N; ii++)
ocp_nlp_out_get(nlp_config, nlp_dims, nlp_out, ii, "u", &utraj[ii*NU]);
ocp_nlp_eval_cost(nlp_solver, nlp_in, nlp_out);
ocp_nlp_get(nlp_solver, "cost_value", &cost_data);
RCLCPP_ERROR(get_logger(), "cost: %f", cost_data);
visualization_msgs::msg::Marker marker;
marker.header.frame_id = "map";
marker.header.stamp = get_clock()->now();
marker.ns = "nmpc path";
marker.id = 42;
marker.type = visualization_msgs::msg::Marker::LINE_STRIP;
marker.color.b = 1.0;
marker.color.a = 1.0;
marker.scale.x = 0.05;
marker.scale.y = 0.05;
marker.scale.z = 0.05;
geometry_msgs::msg::Point point;
for (int i = 0; i <= N; i++) {
point.x = xtraj[i * NX];
point.y = xtraj[i * NX + 1];
point.z = 0.0;
marker.points.push_back(point);
}
marker_publisher_->publish(marker);
printf("\n--- xtraj ---\n");
d_print_exp_tran_mat( NX, N+1, xtraj, NX);
printf("\n--- utraj ---\n");
d_print_exp_tran_mat( NU, N, utraj, NU );
// ocp_nlp_out_print(nlp_solver->dims, nlp_out);
// Publish the control command
ackermann_msgs::msg::AckermannDriveStamped drive_msg;
drive_msg.header.stamp = get_clock()->now();
drive_msg.header.frame_id = "base_link";
drive_msg.drive.speed = u[0];
drive_msg.drive.steering_angle = u[1];
drive_publisher_->publish(drive_msg);
// usleep(3000000);
}
};
int main(int argc, char **argv) {
rclcpp::init(argc, argv);
auto node = std::make_shared<NMPCNode>();
rclcpp::spin(node);
rclcpp::shutdown();
return 0;
}