How to stop the solver after a certain time to guarantee constant Control frequency?

User Questions
1

Hi :wave:

I am implementing a MPC tracking controller for an hexarotor drone using acados Python interface.
For the moment I tested simple (but dynamically unfeasible) trajectories such as steps in position and the control works fine.
The state is in R^13 (position, attitude in quaternions, linear and angular velocities) while the input is in R^6 (six rotor thrusts). I am using the RTI and NONLINEAR_LS cost.
The reference signal to track is sampled at 100 Hz. The prediction horizon is 1 second with 20 shooting nodes, hence at each control iteration the reference at the current sample is read to compute the tracking error and its next 1 second is downsampled at 20 Hz to fill the prediction horizon reference (I use parameters for this).
I run a Gazebo simulation to which I feed the inputs computed by the MPC, so I don’t use acados to integrate the dynamics to simulate the system (this is done by gazebo) and the software framework I am using implements also state estimation and other components.

When the simulation ends I plot the statistics obtained with ocp_solver.get_stats('time_tot') for both preparation and feedback phases. An example of the total execution time (preparation+feedback) is as follows

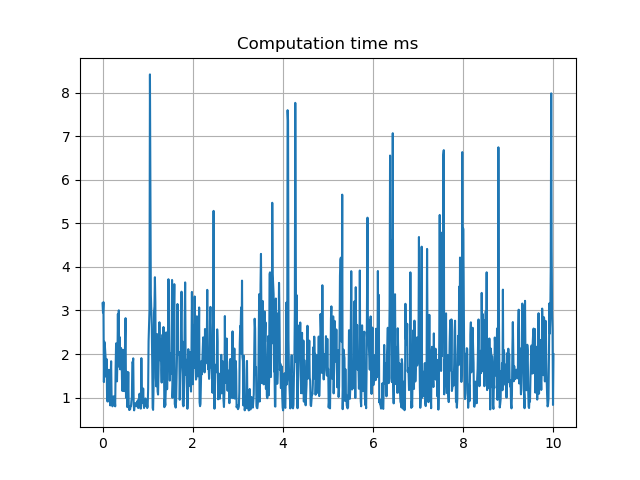
tilthex_circle_MPC_time

There are some spikes > 7 ms, but the average time is lower (around 2 ms).
What I am doing now to manage the control frequency is (in pseudo code):

Given control period T = 10 ms
for i in range(sim):
    solve_mpc()
    t_elapsed = get_time_stats()
    diff_t = T - t_elapsed
    sleep(diff_t)

Since the period T = 10 ms is very conservative, in order to improve the control frequency I could stop the solver after a certain amount of time (say, 5 ms): if it has been able to converge in less time no problem, otherwise some works in literature suggest to use u_k = u_1,k-1.

The questions are:

  • How to check if after a certain time the solver has converged and stop it if not?
  • Are there better ways to guarantee a fixed (non conservative) frequency for the MPC? Are there better ways to manage deadline miss?

Thanks for replies and suggestions,
Lorenzo

2

Hi,

This sounds like a nice application of acados!
The topic has been discussed already here

Overall, the spikes should come only from the QP solver, as all other parts of the algorithm have a deterministic runtime. Maybe you can assess this, by logging time_qp.

3

Thanks! I will investigate further.
When you say that some algorithm have a deterministic runtime, do you mean from a theoretical point of view? Because unless we use a real-time operating system I think a normal OS does not give guarantees in this sense

4

Yes, of course.
I think on a “normal OS” there is no way to guarantee that, the OS can always interrupt your process by something with a higher priority I guess.

5

Clear, thanks again!

6

Hi

We have a similar issue. We understand it is not possible to predict the runtime of the QP-solver, but maybe we could have a time-based termination of SQP iterations to supplement the iteration based termination?

For instance stop iterating if number of iterations > max iterations or total solve time > max solve time.

This does not provide a guarantee, but at least it puts a soft limit on the time spent executing the algorithm.

7

Hi, yes what you are proposing could be good, unfortunately I don’t know if it’s possible.
If you select the maximum number of iterations the solver will exit with an error if a solution is not found within that number.
Also the selection of a predefined stop time is not a possible option.
The only thing I can suggest to obtain more regular computation times is in my previous post:

basically avoiding the sleep function I obtained shorter and more regular computation times.

Hope it can help,

Lorenzo