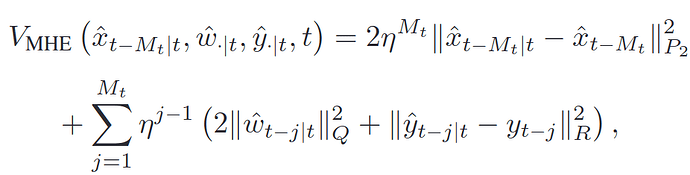Formulate the cost function for mhe

User Questions
1

Hi :wave:

I have known, how to formulate the mhe problem using acados python interface based on the official example.

Now I want try to use a different cost function.

image
image926×236 19 KB

(from J. D. Schiller, S. Muntwiler, J. Köhler, M. N. Zeilinger and M. A. Müller, “A Lyapunov Function for Robust Stability of Moving Horizon Estimation,” in IEEE Transactions on Automatic Control, vol. 68, no. 12, pp. 7466-7481, Dec. 2023, doi: 10.1109/TAC.2023.3280344.},

As the pictures shows, compare to the standard cost function, at the first node, a constant 2*eta**M should be multiplied. And at the intermediate nodes should varying coefficients be multiplied by every different stage. I have read the acados Documentation, according to my understanding, the function" cost_set" be applied to set a scaling. I have formulate the mhe algorithm like this:

in mhe solver:

# Initial cost
ocp_mhe.cst.cost_type_0 = "NONLINEAR_LS"
ocp_mhe.cost.W_0 = block_diag(R, 2*Q, 2*P)
ocp_mhe.model.cost_y_expr_0 = vertcat(ymeas, u, x)
ocp_mhe.cost.yref_0 = np.zeros((ny_0,))

# intermediate
ocp_mhe.cost.cost_type = 'NONLINEAR_LS'
ocp_mhe.cost.W = block_diag(R, 2*Q)
ocp_mhe.model.cost_y_expr = vertcat(ymeas, u)
ocp_mhe.parameter_values = np.zeros((nparam, ))
ocp_mhe.cost.yref = np.zeros((ny,))

in the test code for closed loop:

   # set measurements
    yref_0[:ny] = simY[k, :]
    yref_0[ny+nw:] = x0_bar 
    acados_mhe_solver.set(0, "yref", yref_0)  

    acados_mhe_solver.cost_set(0, "scaling",1/Ts*eta**N_mhe)  ####

    # set controls
    acados_mhe_solver.set(0, "p", simU[k,:])

    for j in range(1, N_mhe):
        # set measurements
        yref[:ny] = simY[k+j, :]
        acados_mhe_solver.set(j, "yref", yref)

        acados_mhe_solver.cost_set(j, "scaling",1/Ts*eta**(N_mhe-j)) ####

        # set controls
        acados_mhe_solver.set(j, "p", simU[k+j,:])

“Note: by default the cost is scaled with the time step, and the terminal cost term scaled with 1. This can be overwritten by setting the ‘scaling’ field.” According this, the time step 1/Ts has been also be multiplied.

The algorithm has given a good results, but I am not sure, is this formulation right?

I am also thinking, should I using external function for cost ? I have find the function to define the type of external cost function. But how to formulate a external cost function. just formulate a cost function expression including wights matrix using casadi, and give it to the “model.cost_y_expr”?
If this idea is correct, could you please provide me an example?

Thanks.
Lingbing

2

Looks good to me!

3

Hi,

so the idea- though “cost_set()” to set “scaling” per stage to multiply a coefficient - is right?

I want to confirm something. in the cost function by default exists a “0.5” . If I set the “scaling” to reformulate the cost function, the “0.5” will be neglected automatic? or should I extra multiply by 2 to compensate it?

best regards
Lingbing

4

Yes exactly, the Implementation via cost scaling is a good idea. The cost is internally multiplied with 0.5 but this does not change the solution.

1 Like